Урок 31. Определение подобных треугольников
Поурочное планирование по геометрии для 8 класса. Ориентировано на работу с УМК Атанасян и др. Геометрия 8 класс. Глава VII. ПОДОБНЫЕ ТРЕУГОЛЬНИКИ. Урок 31. Определение подобных треугольников. Вернуться к Списку уроков Тематического планирования.
Урок 31. Определение подобных треугольников
Основные дидактические цели урока: ввести понятие пропорциональных отрезков и подобных треугольников; рассмотреть свойство биссектрисы треугольника и показать его применение в процессе решения задач.
Ход урока
I. Организационный момент.
Мотивация к учебной деятельности. Учитель сообщает тему урока, формулирует цели урока.
II. Актуализация знаний учащихся
1. Анализ ошибок, допущенных в контрольной работе.
- 1) Провести общий анализ контрольной работы.
- 2) Решить задачи, с которыми не справилось большинство учащихся.
- 3) Работа над ошибками.
(На интерактивной доске записаны готовые ответы и указания к задачам контрольной работы № 2. Ученики находят и исправляют свои ошибки. Учитель по мере необходимости оказывает индивидуальную помощь.)
2. Подготовка учащихся к восприятию нового материала (фронтальная работа).
1) Что называют отношением двух чисел? Что показывает отношение?
2) АВ : CD = 2:1. О чем это говорит? Найдите отношение CD к АВ.
3) В ΔАВС АВ : ВС : АС = 2 : 4 : 3, РАВС = 45 дм. Найдите стороны треугольника АВС.
4) Что называют пропорцией? Верны ли пропорции 1,5 : 1,8 = 25 : 30; 18 : 3 = 5 : 30?
5) В пропорции a: b = c : d укажите крайние и средние члены. Сформулируйте основное свойство пропорции.
6) Переставив средние или крайние члены пропорции, составьте три верные пропорции:
а) 12 : 0,2 = 30 : 0,5;
б) АВ : MN = CD : КР.
7) Найдите неизвестный член пропорции.
а) 7х : 4,2= 12,3 : 6;
б) х : АВ = MN : КР (найти поочередно АВ, MN, КР).
III. Работа по теме урока
- Ввести понятие отношения отрезков.
Определение: Отношением отрезков АВ и CD называется отношение их длин, т. е. АВ : CD. - Ввести понятие пропорциональных отрезков.
Определение: Отрезки АВ и CD пропорциональны отрезкам A1B1 и С1D1 , если AB/A1B1 = СD/С1D1.
Например: Если АВ = 5 см, CD = 7 см, А1В1 = 7,5 см, C1D1 = 10,5 см, то АВ : A1B1 = CD : С1D1, т. е. отрезки АВ и CD пропорциональны отрезкам A1B1 и С1D1.
Отрезки АВ, CD, MN пропорциональны отрезкам A1B1, С1D1, и M1N1. Найдите С1D1 и MN, если AB = 5 см, A1B1 = 20 см, CD = 6 см, M1N1 = 8 см.
- Ввести понятие подобных фигур (два круга, два квадрата, два мяча разных размеров, одна и та же фотография на фотоаппарате и на экране компьютера и т. д.).
- Ввести понятие подобных треугольников.
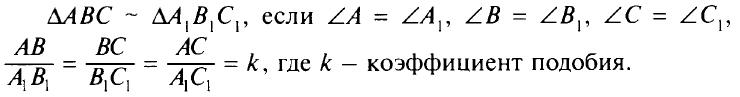
Стороны АВ и A1B1, ВС и B1C1, АС и A1C1, называют сходственными.
Определение: Два треугольника называются подобными, если их углы соответственно равны и стороны одного треугольника пропорциональны сходственным сторонам другого.
IV. Закрепление изученного материала
- Работа в рабочих тетрадях (работа в парах). Решить задачи № 51, 52. (Учитель читает условие задачи № 51, ученики заполняют пропуски в тетради. Одна пара отвечает на вопрос, затем идет обсуждение. Так же решить задачу № 52.)
- Решить задачу № 535. (Ученики самостоятельно читают задачу и ее решение. Один ученик работает у доски, остальные — в тетрадях.)
Вопросы, контролирующие глубину усвоения доказательства.

- Решить на доске и в тетрадях задачи № 536 (б), 541. (Два ученика работают у доски, остальные — в тетрадях.)
Задача № 536 (б)

Наводящие вопросы.
- Как биссектриса треугольника делит противолежащую сторону?
- Длину какого отрезка необходимо найти для нахождения отрезка CD?
- Как можно вычислить длину отрезка ВС?
Задача № 541

Наводящие вопросы.
- Когда два треугольника подобны?
- Равны ли углы этих треугольников?
- Пропорциональны ли сходственные стороны данных треугольников?
- Подобны ли ΔАВС и ΔEDF?
- Решить задачи № 534 (в), 537 (самостоятельно).

V. Рефлексия учебной деятельности
- Что вы понимаете под «отношением отрезков»?
- Что значит «отрезки АВ и CD пропорциональны отрезкам А1В1 и C1D1?
- Приведите примеры подобных фигур.
- Какие треугольники называются подобными?
Домашнее задание
- П. 58, 59, вопросы 1, 2, 3 (учебник, с. 158).
- Решить задачи № 534 (а, б), 535 (устно), 536 (а), 538, 542.
- Решить задачу № 53 (рабочая тетрадь).
Вы смотрели: Поурочное планирование по геометрии для 8 класса. УМК Атанасян и др. (Просвещение). Глава VII. ПОДОБНЫЕ ТРЕУГОЛЬНИКИ. Урок 31. Определение подобных треугольников.
Вернуться к Списку уроков Тематического планирования.