Геометрическая прогрессия
Геометрическая прогрессия
Коды ОГЭ по математике: 4.2.3. Геометрическая прогрессия. Формула общего члена геометрической прогрессии. 4.2.4. Формула суммы первых нескольких членов геометрической прогрессии
Определения и обозначения
Определение. Геометрической прогрессией называют последовательность, каждый член которой, начиная со второго, равен предыдущему члену, умноженному на одно и то же не равное нулю число. (Первый член геометрической прогрессии также не может быть равен нулю.)
В геометрической прогрессии отношение любого члена, начиная со второго, к предыдущему члену равно одному и тому же числу. Это число называют знаменателем геометрической прогрессии и обозначают буквой q. Правило, по которому образуются члены геометрической прогрессии, можно записать в виде рекуррентной формулы: ![]()
Или bn+1 = bn • q.
Пример 1. Пусть b1 = 1 и q = 3. Получаем геометрическую прогрессию: 1; 3; 9; 27; 81; 243; … Это возрастающая последовательность.
Пример 2. Пусть b1 = 5 и q = –2. В этом случае знаки у членов прогрессии чередуются: 5; –10; 20; –40; 80; –160; 320; … . Это последовательность не является ни возрастающей, ни убывающей.
Геометрическая прогрессия, члены которой – положительные числа, обладает свойством: любой её член, начиная со второго, равен среднему геометрическому предыдущего и последующего членов, т. е.
![]()
Формулы n–го члена геометрической прогрессий
Формула n–го члена геометрической прогрессии (bn), первый член которой равен b1, a знаменатель равен q:
bn = b1 • qn–1
Формула содержит три переменные. Если известны значения двух из них, то можно вычислить и значение третьей.
Если последовательность (bn) – геометрическая прогрессия, то для любых натуральных n и m верно равенство: bn = bm • qn-m.
Пример 3. В геометрической прогрессии b3 = –1/2, b6 = 4. Найдём b12.
Так как b6 = b3 • q3, то q3 = b6 / b3 = –8. Далее имеем: b12 = b6 • q6 = b6 • (q3)2 = 4 • (–8)2 = 256.
 Изображение членов геометрической прогрессии
Изображение членов геометрической прогрессии
точками на координатной плоскости
Члены числовой последовательности можно изображать точками на координатной плоскости. Для этого по горизонтальной оси откладывают номер члена, a по вертикальной – соответствующий член последовательности.
На рисунке точками изображены несколько членов геометрической прогрессии (bn), в которой b1 = 1, q = 2; эта прогрессия задаётся формулой
bn = 2n-1.
Скорость её роста всё время увеличивается, и точки, соответствующие её членам, резко «уходят» вверх. Все они лежат на кривой, которая носит название экспонента. Чем выше поднимается экспонента у = 2х, тем круче она становится.
Формула суммы первых n членов геометрической прогрессии
Если q ≠ 1, то ![]()
Заметим, что если 0 < q < 1, то удобнее пользоваться формулой суммы, представленной в виде: ![]()
Если q = 1, то все члены прогрессии равны между собой и Sn = nb1.
Пример 4. Найдём сумму ![]()
Слагаемые в этой сумме – члены геометрической прогрессии, первый член которой равен 1, a знаменатель равен ½. Всего суммируется 11 членов. Имеем:
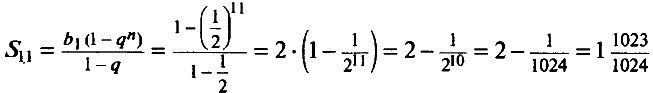
Пример 5. Найдём сумму первых восьми членов геометрической прогрессии, второй член которой равен 6, a четвёртый равен 24.
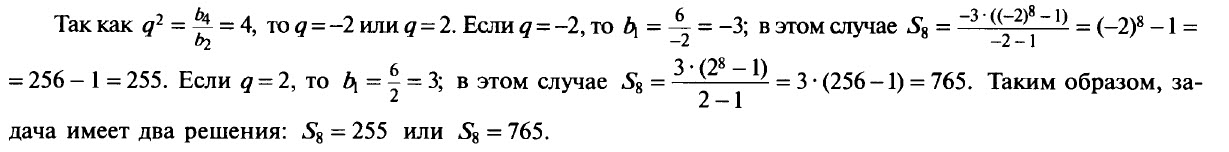
Это конспект по математике на тему «Геометрическая прогрессия». Выберите дальнейшие действия:
- Перейти к следующему конспекту:
- Вернуться к списку конспектов по Математике.
- Проверить знания по Математике.