Формулы сокращенного умножения

ФОРМУЛЫ СОКРАЩЕННОГО УМНОЖЕНИЯ

Умножение многочлена на многочлен

[button title=»! Чтобы умножить многочлен на многочлен, нужно каждое слагаемое одного многочлена умножить на каждое слагаемое другого многочлена и полученные произведения сложить.» color=»blue» size=»2″ full_width=»1″]

Будьте внимательны! У каждого слагаемого есть свой знак.

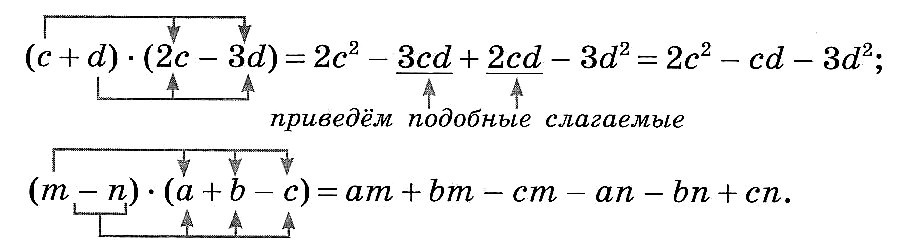
Формулы сокращённого умножения многочленов — это, как правило, 7 (семь) часто встречающихся случаев умножения многочленов.

Определения и Формулы сокращенного умножения. Таблица

Три формулы сокращенного умножения для квадратов

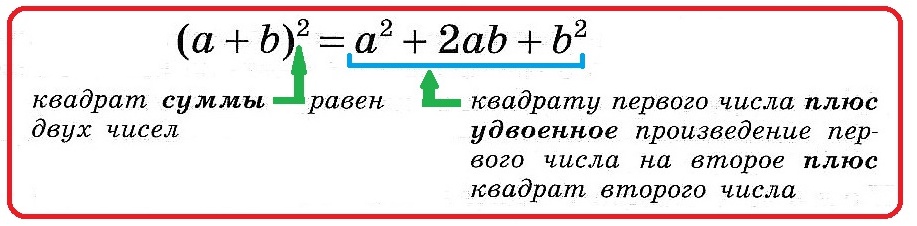
1. Формула квадрата суммы. 

[button title=»Квадрат суммы двух выражений равен квадрату первого выражения плюс удвоенное произведение первого выражения на второе плюс квадрат второго выражения.» color=»blue» size=»2″ full_width=»1″]

Чтобы лучше понять формулу, сначала упростим выражение (развернем формулу квадрата суммы)

А теперь разложим на множители (свернем формулу)

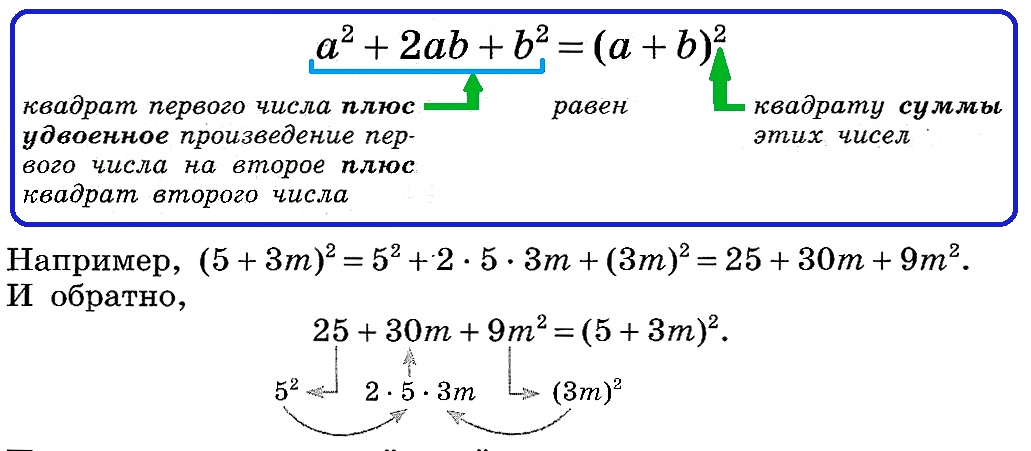
Последовательность действий при разложении на множители:

1. определи, какие одночлены возводились в квадрат (5 и 3m);
2. проверь, стоит ли в середине формулы их удвоенное произведение (2 • 5 • 3m = 30m);
3. запиши ответ (5 + 3m)².

2. Формула квадрата разности

[button title=»Квадрат разности двух выражений равен квадрату первого выражения минус удвоенное произведение первого выражения на второе плюс квадрат второго выражения.» color=»blue» size=»2″ full_width=»1″]

Сначала упростим выражение (развернем формулу):

А потом наоборот, разложим на множители (свернем формулу):

3. Формула разности квадратов

Произведение суммы двух выражений на их разность равно разности квадратов этих выражений.

Свернем формулу (выполним умножение)

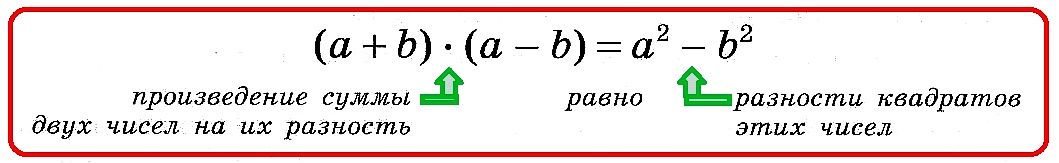
А теперь развернем формулу (разложим на множители)

Четыре формулы сокращенного умножения для кубов

4. Формула куба суммы двух чисел

Куб суммы двух выражений равен кубу первого выражения плюс утроенное произведение квадрата первого выражения на второе плюс утроенное произведение первого выражения на квадрат второго плюс куб второго выражения.

Последовательность действий при «сворачивании» формулы:

1.  найти одночлены, которые возводились в куб (здесь 4х и 1);
2. проверить средние слагаемые на соответствие формуле;
3. записать ответ.

5. Формула куба разности двух чисел

Куб разности двух выражений равен кубу первого выражения минус утроенное произведение квадрата первого выражения на второе плюс утроенное произведение первого выражения на квадрат второго минус куб второго выражения.

6. Формула суммы кубов

Сумма кубов двух выражений равна произведению суммы первого и второго выражения на неполный квадрат разности этих выражений.

И обратно:

7. Формула разности кубов

Разность кубов двух выражений равна произведению разности первого и второго выражения на неполный квадрат суммы этих выражений.

Применение формул сокращенного умножения. Таблица

Пример использования формул на практике (устный счет).

Задача: Найти площадь квадрата со стороной а = 71 см.
Решение: S = a². Используя формулу квадрата суммы, имеем
71² = (70 + 1)² = 70² + 2*70*1 + 1² = 4900 + 140 + 1 = 5041 см²
Ответ: 5041 см²

Конец конспекта урока по алгебре «Формулы сокращенного умножения». Выберите следующие действия:

• Вернуться в раздел Алгебра 7 класс
• Перейти к следующему конспекту «Разложение на множители»
• Проверить знания по Алгебре (онлайн-тесты 7 класс)