Урок 34. Решение задач на применение 1 признака подобия Δ
Поурочное планирование по геометрии для 8 класса. Ориентировано на работу с УМК Атанасян и др. Геометрия 8 класс. Глава VII. ПОДОБНЫЕ ТРЕУГОЛЬНИКИ. Урок 34. Решение задач на применение первого признака подобия треугольников. Вернуться к Списку уроков Тематического планирования.
Урок 34. Решение задач на применение первого признака подобия треугольников
Основная дидактическая цель урока: сформировать у учащихся навыки решения задач на применение первого признака подобия треугольников.
Ход урока
I. Организационный момент.
Мотивация к учебной деятельности (Учитель сообщает тему урока, формулирует цели урока.)
II. Актуализация знаний учащихся
- Теоретический опрос.
1) Доказать теорему, выражающую первый признак подобия треугольников. (Один ученик готовит доказательство теоремы у доски. Заслушать после проведения фронтального теоретического опроса.)
- Фронтальный теоретический опрос.
- Сформулируйте первый признак подобия треугольников.
- Чему равно отношение периметров подобных треугольников?
- Какие треугольники называются подобными?
- Сформулируйте теорему об отношении площадей подобных треугольников.
III. Решение задач по готовым чертежам
Решить задачи (самостоятельно).
(Один ученик вслух читает задачу и ее решение. Учащиеся его слушают, а затем исправляют ошибки. Учитель индивидуально проверяет домашнее задание.)
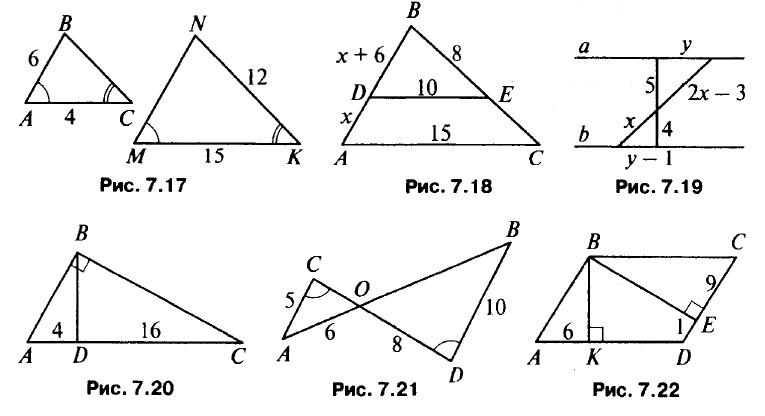
- Рис. 7.17. Найти: ВС, MN.
- Дано: DE||АС (рис. 7.18). Найти: АВ, ВС.
- Дано: а||b (рис. 7.19). Найти: х, у.
- Рис. 7.20. Найти: BD.
- Рис. 7.21. Найти: СО, ВО.
- Рис. 7.22. Найти: ВС.
Ответы к задачам по готовым чертежам:
- ВС =3,2, MN= 22,4.
- АВ= 18, ВС= 12.
- х = 4, у = 5.
- BD = 8.
- СО = 4, ВО = 12.
- ВС= 15.
IV. Решение задач
- Работа в рабочих тетрадях.
Решить задачу № 58. (Учащиеся самостоятельно решают задачу, по окончании работы один ученик вслух читает задачу и ее решение. Учащиеся его слушают, а затем исправляют ошибки.)
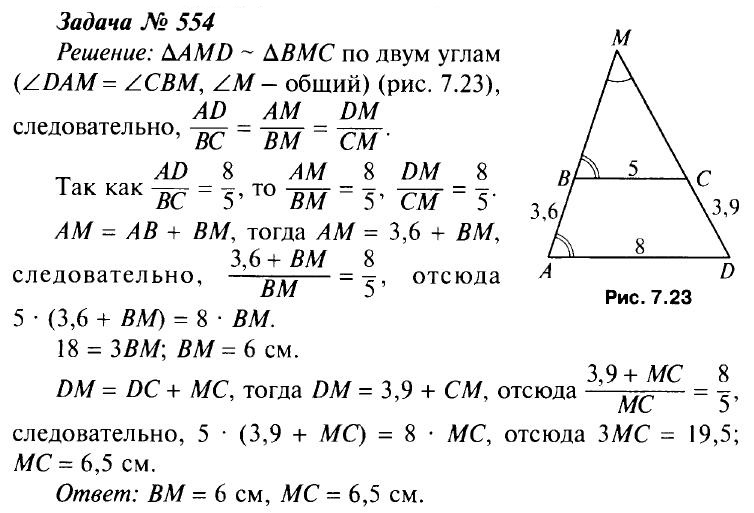
- Решить задачу № 554 (работа в парах).
Наводящие вопросы.
- Есть ли на рисунке подобные треугольники? Почему вы так считаете?
- Найдите коэффициент подобия этих треугольников?
- Каким соотношением связаны сходственные стороны AM и BMP DM и СМ?
- Решить задачу № 556 (с последующим обсуждением решения).
Вопросы для обсуждения.
- Почему ∠O = ∠CАС1? (Это соответственные углы при параллельных прямых АС1 и OD и секущей ОА.)
- Почему ∠OAB = ∠C? (Это соответственные углы при параллельных прямых АВ и CD и секущей АС.)
- Почему ОА : АС = ОВ : АС1? (Это сходственные стороны подобных треугольников.)
- Докажите, что АС1 = BD. (BAC1D — параллелограмм, так как АВ||CD по условию задачи, АС1||BD как противолежащие стороны параллелограмма.)
- Объясните, каким образом из равенств ОА : АС = ОВ : AС1 и AC1 = BD получилось равенство OA : OB = АС : BD.
- Решить задачу N° 557 (а). (На доске подготовить рисунок. Записать краткое решение задачи.)
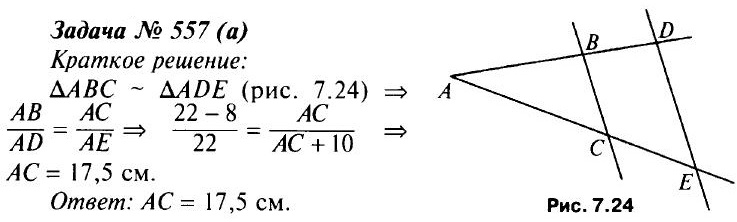
Наводящие вопросы.
- Есть ли на рисунке подобные треугольники? Докажите их подобие.
- Составьте отношение сходственных сторон и найдите АС.
V. Самостоятельное решение задач
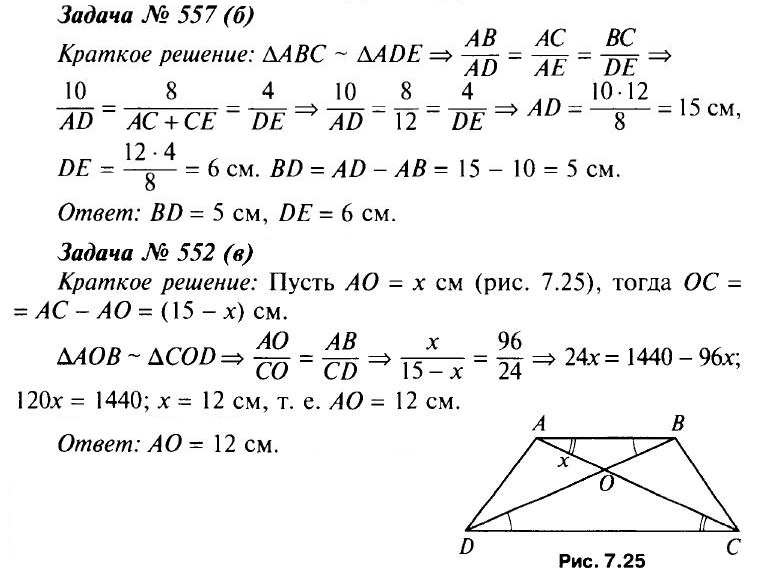
- Решить задачи № 557 (б), 552 (в).
(После окончания самостоятельного решения задач и самопроверки по готовым ответам выполняется самооценка.) Критерии оценивания:
- оценка «5» — правильно решены две задачи;
- оценка «4» — одна из задач решена правильно, а при решении второй задачи допущены незначительные ошибки;
- оценка «3» — правильно решена одна задача или при решении двух задач допущены незначительные ошибки;
- оценка «2» — не ставится.
- Решить дополнительную задачу.
Диагонали трапеции ABCD с основаниями AD и ВС пересекаются в точке О. Периметры треугольников ВОС и AOD относятся как 2 : 3, АС = 20. Найдите длины отрезков АО и ОС.

VI. Рефлексия учебной деятельности
- Сформулируйте первый признак подобия треугольников.
- Сколько пар равных углов нужно найти, чтобы доказать подобие треугольников?
- Сколько пар равных углов нужно найти у прямоугольных (равнобедренных) треугольников, чтобы данные треугольники были подобны?
- Могут ли быть подобными равносторонние треугольники?
Домашнее задание
- Повторить П. 61.
- Решить задачи № 552 (а, б), 557 (в), 558.
- Решить дополнительную задачу.
В трапеции ABCD (AD и ВС — основания) точка К лежит на стороне CD, причем СК : KD = 1 : 2. АК пересекает BD в точке О. Докажите, что если ВС : AD = 1 : 2, ВО = OD.
Вы смотрели: Поурочное планирование по геометрии для 8 класса. УМК Атанасян и др. (Просвещение). Глава VII. ПОДОБНЫЕ ТРЕУГОЛЬНИКИ. Урок 34. Решение задач на применение первого признака подобия треугольников.
Вернуться к Списку уроков Тематического планирования.