Решение неравенств первой степени

Решение неравенств первой степени

Ключевые слова: основные понятия, неравенства первой степени, решение неравенств первой степени, примеры решения задач. Раздел ОГЭ по математике: 3.2.2. Неравенство с одной переменной. Решение неравенства.

Неравенства с одной переменной решают почти так же, как и уравнения. Значение переменной, при подстановке которой в неравенство получается верное числовое неравенство, называется решением неравенства. Решить неравенство – это значит найти все его решения или показать, что их нет.

Неравенства, у которых множества решений совпадают, называют равносильными. При решении неравенств пользуются следующими правилами, которые позволяют заменять одно неравенство другим, ему равносильным:

• члены неравенства можно переносить из одной его части в другую с противоположным знаком;
• обе части неравенства можно умножать или делить на одно и то же положительное число;
• обе части неравенства можно умножать или делить на одно и то же отрицательное число и заменять при этом знак неравенства на противоположный.

Рассмотрим, например, неравенство 3х(х+2) – 20 > 6х+7. Заменим его более простым равносильным ему неравенством:
3х² + 6х – 20 > 6х + 7,
3х² + 6х – 20 – 6х – 7 > 0,
3х²– 27 > 0,
х²– 9 > 0.

Сначала мы раскрыли скобки в левой части неравенства, затем из правой части в левую перенесли слагаемые с противоположными знаками, после приведения подобных разделили обе части неравенства на одно и то же положительное число 3. Получили квадратное неравенство (способ решения таких неравенств в следующем параграфе).

Решение неравенств первой степени

Неравенства первой степени – это неравенства вида ах + b > 0 или ах + b ≥ 0, ах + b < 0, ах + b ≤ 0, где а ≠ 0. Например, неравенства   2х – 3 > 0;   0,3x +1,2 > 0;   5 – 10x ≤ 0 являются неравенствами первой степени.

Решим, например, последнее из этих неравенств: 5 – 10x ≤ 0. Коэффициент при переменной х отрицательный, и всегда полезно сначала «избавиться» от отрицательного коэффициента при х. Для этого можно умножить обе части неравенства на –1 и не забыть заменить знак неравенства на противоположный. Получим: 10х – 5 ≥ 0. (Можно поступить и иначе – перенести –10х в правую часть с противоположным знаком: 5 ≤ 10х.) Далее:  10x ≥ 5,   x ≥ 0,5. Последнее неравенство можно считать ответом, так как оно вполне ясно описывает множество всех значений x, являющихся его решениями. Можно также записать решение неравенства в виде числового промежутка: [0,5; +оо). На координатной прямой множество решений этого неравенства можно показать так:

Множеством решений неравенства первой степени всегда является числовой луч – или с принадлежащим ему началом, как в данном случае, или с непринадлежащим (в случае строгого неравенства).

Примеры решения задач

Пример 1. Определим, в каком случае на координатной прямой изображено множество решений неравенства 19 – 7x > 20 – 3(x – 5).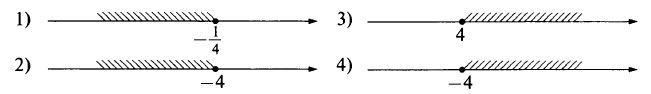

Самая правильная стратегия поиска ответа на вопрос состоит в том, чтобы просто решить неравенство.
19 – 7x > 20 – 3(x – 5),
19 – 7x > 20 – 3x +15,
–4x > 16,
4x < –16,
x < –4.

Ответ: 2.

Пример 2. Решим неравенство 

Сначала «избавимся» от дробей, умножив обе части неравенства на общий знаменатель дробей – число 6. При этом надо быть внимательным и не забыть умножить на 6 первое слагаемое в правой части: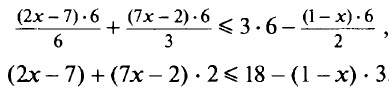

После преобразований получим: х ≤ 2.
Ответ: х ≤ 2.

Пример 3. Решим неравенство 9(6 + 2x) < 4√5(6 + 2х).
Преобразуем неравенство следующим образом:  9(6 + 2х) – 4√5(6 + 2x) < 0 .

Теперь вынесем за скобки общий множитель 6 + 2x, получим: (6 + 2x)(9 – 4√5) < 0. Определим знак разности: 9 – 4√5. Так как 9 = √81, 4√5 = √80 и √81 > √80, то 9 – 4√5 > 0. Разделив обе части неравенства на положительное число 9 – 4√5, получаем неравенство 6 + 2x < 0. Отсюда x < –3.

Ответ: x < –3.

Это конспект по алгебре на тему «Решение неравенств первой степени». Выберите дальнейшие действия:

• Перейти к следующему конспекту: Решение систем неравенств первой степени
• Вернуться к списку конспектов по Математике.
• Проверить знания по Математике.