Решение систем неравенств первой степени

Решение систем неравенств первой степени

Ключевые слова: решение систем неравенств первой степени, двойные неравенства, примеры решения задач. Раздел ОГЭ по математике: 3.2.4. Системы линейных неравенств.

Неравенства с одной переменной решают почти так же, как и уравнения. Значение переменной, при подстановке которой в неравенство получается верное числовое неравенство, называется решением неравенства. Решить неравенство – это значит найти все его решения или показать, что их нет.

Решение неравенств первой степени было рассмотрено ранее. В данном конспекте — решение систем неравенств первой степени.

Когда требуется найти множество значений переменной, удовлетворяющих одновременно двум или нескольким неравенствам, говорят, что надо решить систему неравенств. Общий приём решения системы неравенств состоит в следующем: сначала решаем каждое неравенство отдельно, a затем находим множество их общих решений. При нахождении множества общих решений целесообразно пользоваться координатной прямой как опорным образом – это позволит во многих случаях избежать ошибок.

Примеры решения задач

Пример 1. Решим систему неравенств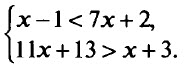

Решив первое неравенство, получим, что х > –0,5, решив второе неравенство, получим, что х > –1. Изобразим на координатной прямой множество решений каждого неравенства.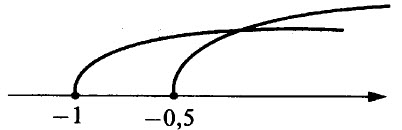

Из рисунка видно, что общей частью этих двух лучей служит множество чисел, больших –0,5.

Ответ: (–0,5; +оо).

Пример 2. Найдём множество решений двойного неравенства –2 < 4 – 3х < 10.

Решить двойное неравенство –2 < 4 – 3х < 10 – это то же самое, что решить систему неравенств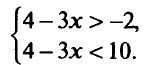

Вы можете сделать это самостоятельно. Но можно вести запись решения и с помощью двойных неравенств:
–2 < 4 – 3х < 10,                   –2 – 4 < –3х < 10 – 4,
–6 < –3х < 6,                         6 > 3х > –6,
–6 < 3х < 6,                           –2 < х < 2.

Ответ: (–2; 2).

Пример 3. Решим задачу: «Боковая сторона равнобедренного треугольника равна 13 см, a его периметр больше 44 см. Какую длину может иметь основание треугольника?»

Для решения составим по условию задачи систему неравенств, используя неравенство треугольника. Пусть длина основания треугольника равна х см. Тогда периметр треугольника равен (х + 26) см и в соответствии с условием х + 26 > 44.

Длина каждой стороны треугольника меньше суммы длин двух других сторон. Поэтому можно составить ещё два неравенства, которым должны удовлетворять искомые величины: х < 26; 13 < х + 13. Получаем систему неравенств: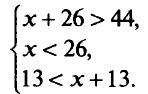

Решив её, получим, что 18 < х < 26.

Ответ: (18; 26).

Это конспект по алгебре на тему «Решение неравенств первой степени». Выберите дальнейшие действия:

• Перейти к следующему конспекту: Квадратные неравенства
• Вернуться к списку конспектов по Математике.
• Проверить знания по Математике.