Мерзляк Геометрия 7 Глава 4 Окружность и круг. Геометрические построения
«Мерзляк Геометрия 7 Глава 4»
Краткий конспект учебника по геометрии за 7 класс (А.Г.Мерзляк и др.) в 4-х частях. Цитаты из учебника помогут учащимся, которые сдали учебник в библиотеку при переходе в старший класс, быстро освежить знания, полученные в 7 классе. Часть 4-я.
Глава 4. Окружность и круг.
Геометрические построения
«Мерзляк Геометрия 7 Глава 4» СОДЕРЖАНИЕ: 19) Геометрическое место точек. Окружность и круг. 20) Некоторые свойства окружности. Касательная к окружности. 21) Описанная и вписанная окружности треугольника. 22) Задачи на построение. 23) Метод геометрических мест точек в задачах на построение.
§ 19. Геометрическое место точек. Окружность и круг
Любое множество точек — это геометрическая фигура. Изобразить произвольную фигуру легко: всё, что нарисуете, — это геометрическая фигура. Однако изучать фигуры, состоящие из хаотически расположенных точек, вряд ли целесообразно. Поэтому разумно выделить тот класс фигур, все точки которых обладают каким-то характерным свойством. Каждую из таких фигур называют геометрическим местом точек.
Определение.
Геометрическим местом точек (ГМТ) называют множество всех точек, обладающих определённым свойством.




§ 20. Некоторые свойства окружности. Касательная к окружности



§ 21. Описанная и вписанная окружности треугольника



§ 22. Задачи на построение
При построении фигур в геометрии принимают такие правила:
1) все построения выполняются только с помощью циркуля и линейки без делений;
2) с помощью линейки можно через заданную точку провести произвольную прямую, а также через заданные две точки А и В провести прямую АВ.
3) с помощью циркуля можно построить окружность с данным центром и радиусом, равным заданному отрезку.
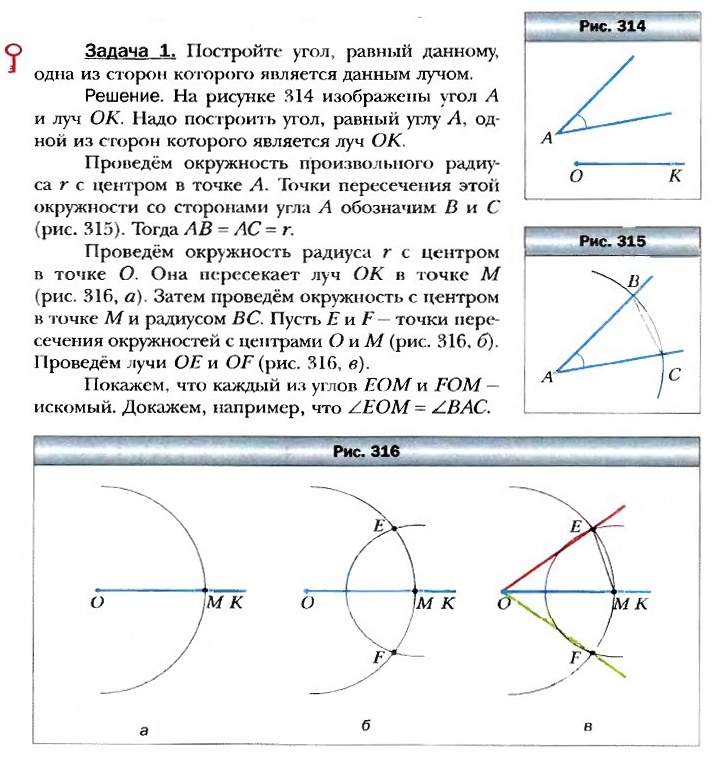




§ 23. Метод геометрических мест точек в задачах на построение
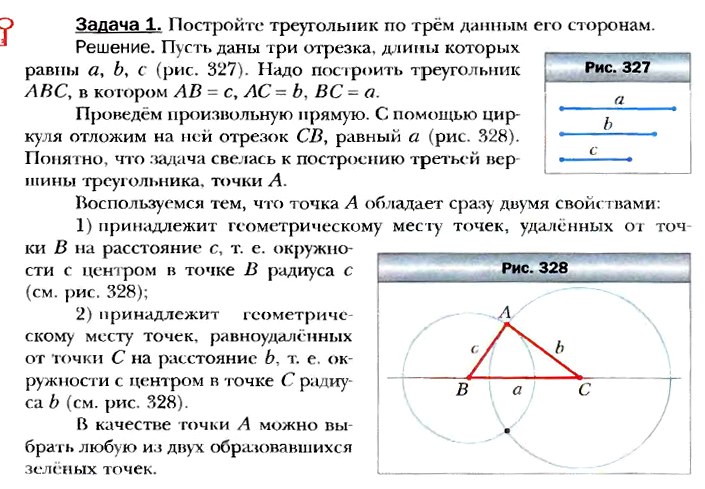

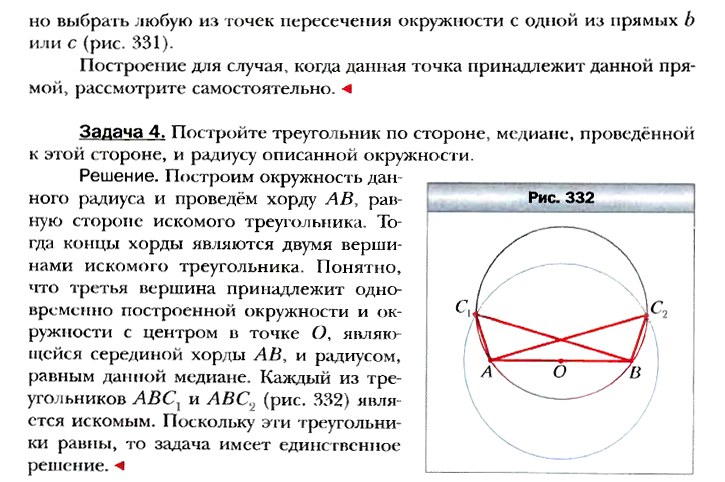
ИТОГИ ГЛАВЫ 4.
Геометрическое место точек (ГМТ)
Геометрическим местом точек (ГМТ) называют множество всех точек, обладающих определённым свойством.
Серединный перпендикуляр отрезка как ГМТ
Серединный перпендикуляр отрезка является геометрическим местом точек, равноудалённых от концов этого отрезка.
Биссектриса угла как ГМТ
Биссектриса угла является геометрическим местом точек, принадлежащих углу и равноудалённых от его сторон.
Окружность
Окружностью называют геометрическое место точек, равноудалённых от заданной точки.
Круг
Кругом называют геометрическое место точек, расстояние от которых до заданной точки не больше данного положительного числа.
Хорда окружности
Отрезок, соединяющий две точки окружности, называют хордой окружности.
Диаметр окружности
Хорду, проходящую через центр окружности, называют диаметром.
Свойства окружности
Диаметр окружности, перпендикулярный хорде, делит эту хорду пополам.
Диаметр окружности, делящий пополам хорду, отличную от диаметра, перпендикулярен этой хорде.
Касательная к окружности
Прямую, имеющую с окружностью только одну общую точку, называют касательной к окружности.
Свойство касательной
Касательная к окружности перпендикулярна радиусу, проведённому в точку касания.
Признак касательной к окружности
Если прямая, проходящая через точку окружности, перпендикулярна радиусу, проведённому в эту точку, то эта прямая является касательной к данной окружности.
Если расстояние от центра окружности до некоторой прямой равно радиусу окружности, то эта прямая является касательной к данной окружности.
Окружность, описанная около треугольника
Окружность называют описанной около треугольника, если она проходит через все вершины этого треугольника. Около любого треугольника можно описать окружность.
Центр окружности, описанной около треугольника
Центр окружности, описанной около треугольника, — это точка пересечения серединных перпендикуляров его сторон.
Окружность, вписанная в треугольник
Окружность называют вписанной в треугольник, если она касается всех его сторон.
В любой треугольник можно вписать окружность.
Центр окружности, вписанной в треугольник
Центр окружности, вписанной в треугольник, — это точка пересечения его биссектрис.
Это конспект по теме «Мерзляк Геометрия 7 Глава 4». Выберите дальнейшие действия:
- Перейти Главе 1 «Простейшие геометрические фигуры»
- Перейти Главе 2 «Треугольники»
- Перейти Главе 3 «Параллельные прямые. Сумма углов треугольника»
- Вернуться к Списку конспектов по геометрии