Мерзляк Геометрия 7 Глава 2 Треугольники
«Мерзляк Геометрия 7 Глава 2»
Краткий конспект учебника по геометрии за 7 класс (А.Г.Мерзляк и др.) в 4-х частях. Цитаты из учебника помогут учащимся, которые сдали учебник в библиотеку при переходе в старший класс, быстро освежить знания, полученные в 7 классе. Часть 2-я.
Глава 2. Треугольники
СОДЕРЖАНИЕ: 7) Равные треугольники. Высота, медиана, биссектриса треугольника. 8) Первый и второй признак равенства треугольников. 9) Равнобедренный треугольник и его свойства. 10) Признаки равнобедренного треугольника. 11) Третий признак равенства треугольников. 12) Теоремы.
§ 7. Равные треугольники. Высота, медиана, биссектриса треугольника
Рассмотрим три точки А, В, С, не лежащие на одной прямой. Соединим их отрезками АВ, ВС, СА. Полученная фигура ограничивает часть плоскости, выделенную на рисунке 108 зеленым цветом. Эту часть плоскости вместе с отрезками АВ, ВС и СА называют треугольником.
Точки А, В, С называют вершинами, а отрезки АВ, ВС, СА — сторонами треугольника. Треугольник называют и обозначают по его вершинам. Треугольник, изображённый на рисунке 108, обозначают так: ΔАВС, или ΔВСА, или ΔАСВ (читают: «треугольник АВС», «треугольник ВСА», «треугольник АСВ»).
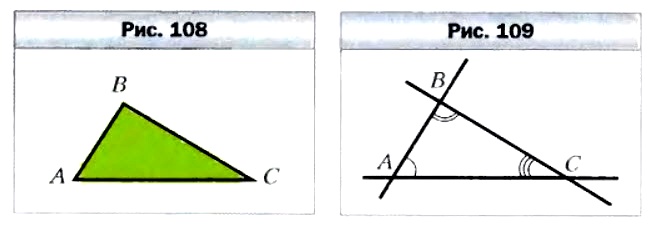
Углы ВАС, АВС, ВСА (рис. 109) называют углами треугольника АВС. В треугольнике АВС (рис. 109), например, угол В называют , противолежащим стороне АС, углы А и С — углами, прилежащими к стороне АС, сторону АС — стороной, противолежащей углу В, стороны АВ и АС — сторонами, прилежащими к углу А.

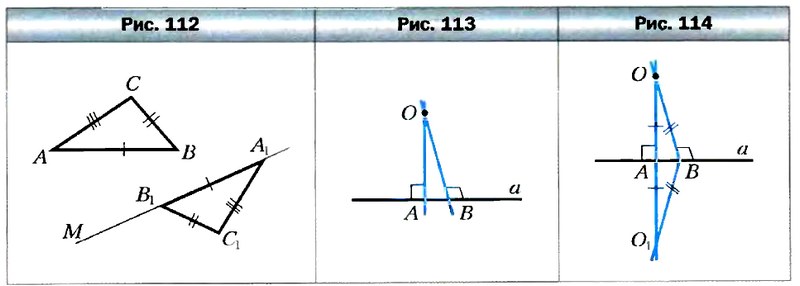


§ 8. Первый и второй признак равенства треугольников



§ 9. Равнобедренный треугольник и его свойства
Определение. Треугольник, у которого две стороны равны, называют равнобедренным.
Равные стороны треугольника называют боковыми сторонами, а третью сторону — основанием равнобедренного треугольника. Вершиной равнобедренного треугольника называют общую точку его боковых сторон. При этом угол В называют углом при вершине, а углы А и С — углами при основании равнобедренного треугольника.
Определение. Треугольник, у которого все стороны равны, называют равносторонним.
Равносторонний треугольник — частный случай равнобедренного треугольника.

§ 10. Признаки равнобедренного треугольника




§ 11. Третий признак равенства треугольников


§ 12. Теоремы
Формулировки всех теорем, которые мы доказали, состоят из двух частей. Первую часть теоремы (то, что дано) называют условием теоремы, вторую часть теоремы (то, что требуется доказать) — заключением.
Например, в теореме 8.1 (первый признак равенства треугольников) условием является то, что две стороны и угол между ними одного треугольника равны двум сторонам и углу между ними другого треугольника, а заключением — равенство
ников.
Все знакомые вам теоремы можно условно разделить на теоремы-свойства и теоремы-признаки. Например, теорема 1.1 устанавливает свойство пересекающихся прямых, теорема 9.1 — свойство равнобедренного треугольника.
Теоремы-признаки перечисляют свойства, по которым можно распознать фигуру, т. е. отнести её к тому или иному виду (классу). Так, теоремы-признаки равенства треугольников указывают требования, по которым два треугольника можно причислить к классу равных. Например, в теоремах 10.1-10.4 сформулированы свойства, по которым распознают равнобедренный треугольник.
Теоремы, которые следуют непосредственно из аксиом или теорем, называют теоремами-следствиями или следствиями. Например, свойство углов, противолежащих равным сторонам треугольника, является следствием из теоремы 9.1.
Если в теореме 8.2 о свойстве серединного перпендикуляра поменять местами условие и заключение, то получим теорему 11.2. Такие теоремы называют взаимно обратными. Если какую-то из этих теорем назвать прямой, то вторую теорему будем называть обратной.
Меняя местами условие и заключение теоремы, надо быть очень внимательными: не всегда можно получить истинное утверждение. Например, утверждение, обратное теореме 4.1 о сумме смежных углов, неверно. Действительно, если сумма каких-то двух углов равна 180°, то совершенно не обязательно, чтобы эти углы были смежными.
Вы знаете, что справедливость теоремы устанавливают путём логических рассуждений, т. е. доказательства. Теорема 1.1 была доказана методом от противного. Название этого метода фактически отражает его суть. Мы предположили, что заключение теоремы 1.1 неверно. На основании этого предположения с помощью логических рассуждений был получен факт, который противоречил основному свойству прямой.
Методом от противного также были доказаны и другие теоремы, например теоремы 5.1, 10.3. Очень важно, чтобы доказательство теоремы было полным, т. е. рассмотрены все возможные случаи. Так, полное доказательство теоремы 11.1 (третий признак равенства треугольников) потребовало рассмотрения всех трёх возможных случаев.
Умение видеть все тонкости и нюансы доказательства — важнейшее качество, формирующее математическую культуру. Если бы, например, при доказательстве теоремы 8.2 о свойстве серединного перпендикуляра мы не рассмотрели отдельно случай, когда точка X является серединой отрезка то обращение к треугольникам АХМ и ВХМ было бы не совсем «законным».
При доказательстве теоремы 10.4 (признак равнобедренного треугольника) мы использовали приём дополнительного построения: чертёж дополнили элементами, о которых не шла речь в условии теоремы. Этот метод является ключом к решению многих задач и доказательству ряда теорем. Поэтому очень важно научиться видеть «выгодное» (результативное) дополнительное построение.
ИТОГИ ГЛАВЫ 2.
Определение. Равные фигуры
Две фигуры называют равными, если их можно совместить наложением.
Основное свойство равенства треугольников
Для данного треугольника АВС и луча А1М существует треугольник A1B1C1 равный треугольнику АВС, такой, что АВ = А1В1, ВС = В1С1, АС = А1С1 и сторона A1B1 принадлежит лучу А1М, а вершина С1 лежит в заданной полуплоскости относительно прямой А1М.
ТЕОРЕМА 7.1. О единственности прямой, перпендикулярной данной
Через точку, не принадлежащую данной прямой, проходит только одна прямая, перпендикулярная данной.
Высота треугольника
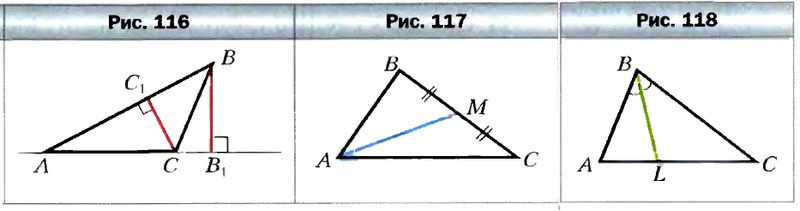
Перпендикуляр, опущенный из вершины треугольника на прямую, содержащую противолежащую сторону, называют высотой треугольника.
Медиана треугольника
Отрезок, соединяющий вершину треугольника с серединой противолежащей стороны, называют медианой треугольника.
Биссектриса треугольника
Отрезок биссектрисы угла треугольника, соединяющий вершину треугольника с точкой противолежащей стороны, называют биссектрисой треугольника.
ТЕОРЕМА 8.1. Первый признак равенства треугольников: по двум сторонам и углу между ними
Если две стороны и угол между ними одного треугольника равны соответственно двум сторонам и углу между ними другого треугольника, то такие треугольники равны.
Серединный перпендикуляр отрезка
Прямую, перпендикулярную отрезку и проходящую через его середину, называют серединным перпендикуляром отрезка.
ТЕОРЕМА 8.2.
Каждая точка серединного перпендикуляра отрезка равноудалена от концов этого отрезка.
ТЕОРЕМА 8.3. Второй признак равенства треугольников: по стороне и двум прилежащим к ней углам
Если сторона и два прилежащих к ней угла одного треугольника равны соответственно стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны.
Равнобедренный треугольник
Треугольник, у которого две стороны равны, называют равнобедренным.
Равносторонний треугольник
Треугольник, у которого все стороны равны, называют равносторонним.
ТЕОРЕМА 9.1. Свойства равнобедренного треугольника
В равнобедренном треугольнике: 1) углы при основании равны; 2) биссектриса треугольника, проведённая из угла при вершине, является медианой и высотой.
Свойства треугольников, следующие из свойств равнобедренного треугольника
• В треугольнике против равных сторон лежат равные углы.
• В равнобедренном треугольнике биссектриса, высота и медиана, проведённые из его вершины, совпадают.
• В равностороннем треугольнике все углы равны.
• В равностороннем треугольнике биссектриса, высота и медиана, проведённые из одной вершины, совпадают.
Признаки равнобедренного треугольника
• Если медиана треугольника является его высотой, то этот треугольник равнобедренный (Теорема 10.1)
• Если биссектриса треугольника является его высотой, то этот треугольник равнобедренный (Теорема 10.2)
• Если в треугольнике два угла равны, то этот треугольник равнобедренный (Теорема 10.3)
• Если медиана треугольника является его биссектрисой, то этот треугольник равнобедренный (Теорема 10.4)
ТЕОРЕМА 11.1.Третий признак равенства треугольников: по трём сторонам
Если три стороны одного треугольника равны соответственно трём сторонам другого треугольника, то такие треугольники равны.
Это конспект по теме «Мерзляк Геометрия 7 Глава 2». Выберите дальнейшие действия:
- Перейти Главе 1 «Простейшие геометрические фигуры»
- Перейти Главе 3 «Параллельные прямые. Сумма углов треугольника»
- Перейти Главе 4 «Окружность и круг. Геометрические построения»
- Вернуться к Списку конспектов по геометрии