Ломаная. Многоугольник + ЗАДАЧИ
«Ломаная. Многоугольник
+ ключевые ЗАДАЧИ»
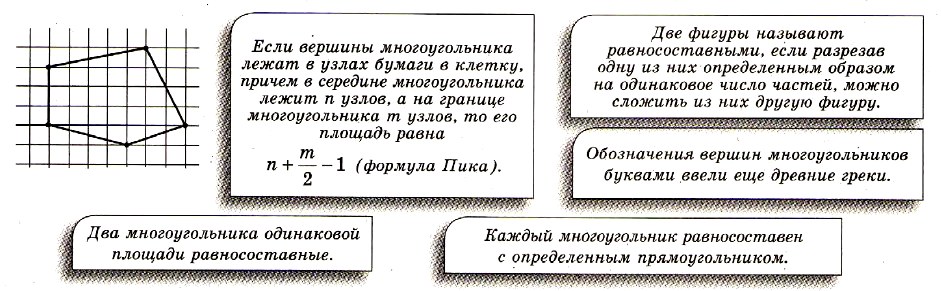
ОПРЕДЕЛЕНИЯ
Ломаная А1А2А3…Аn — фигура, состоящая из точек А1, А2, А3, …, Аn и отрезков А1А2, А2А3, …, Аn-1Аn, которые их соединяют. Точки А1, А2, А3, …, Аn называют вершинами ломаной, а отрезки А1А2, А2А3, …, Аn-1Аn — звеньями ломаной.
Простая лoманая — лoманая, не имеющая точек самопересечения.
Замкнутая лoманая — лoманая, концы которой соединяются.
Длина ломаной — сумма длин ее звеньев.
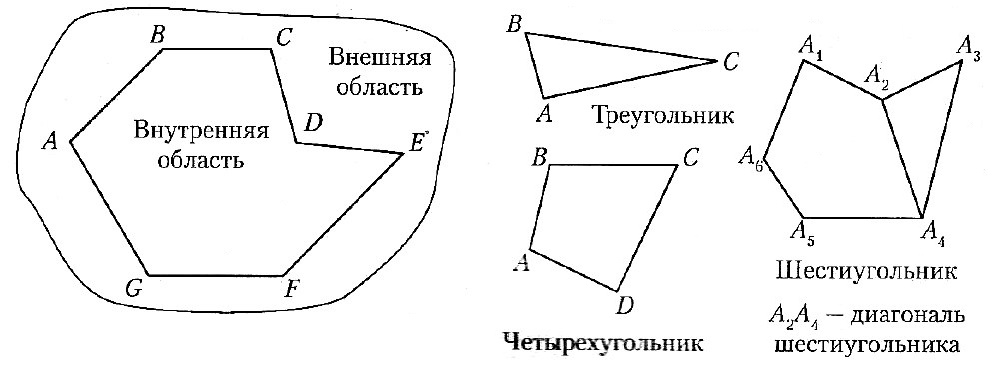
Многоугольник — простая замкнутая ломаная, соседние звенья которой не лежат на одной прямой; вершины ломаной называют вершинами многоугольника, а звенья ломаной — сторонами многоугольника. Многоугольник с n вершинами (n сторонами) называют n-угольником.
Диагональ многоугольника — отрезки, соединяющие несоседние вершины многоугольника.
Выпуклый многoугольник — многоугoльник, лежащий в одной полуплоскости относительно любой прямой, содержащей его сторону.
Угол выпуклого многоугольника при данной вершине — угол, образованный его сторонами, сходящимися в этой вершине.
Внешний угол выпуклого многоугольника при данной вершине — угол, смежный с внутренним углом многоугольника при этой вершине.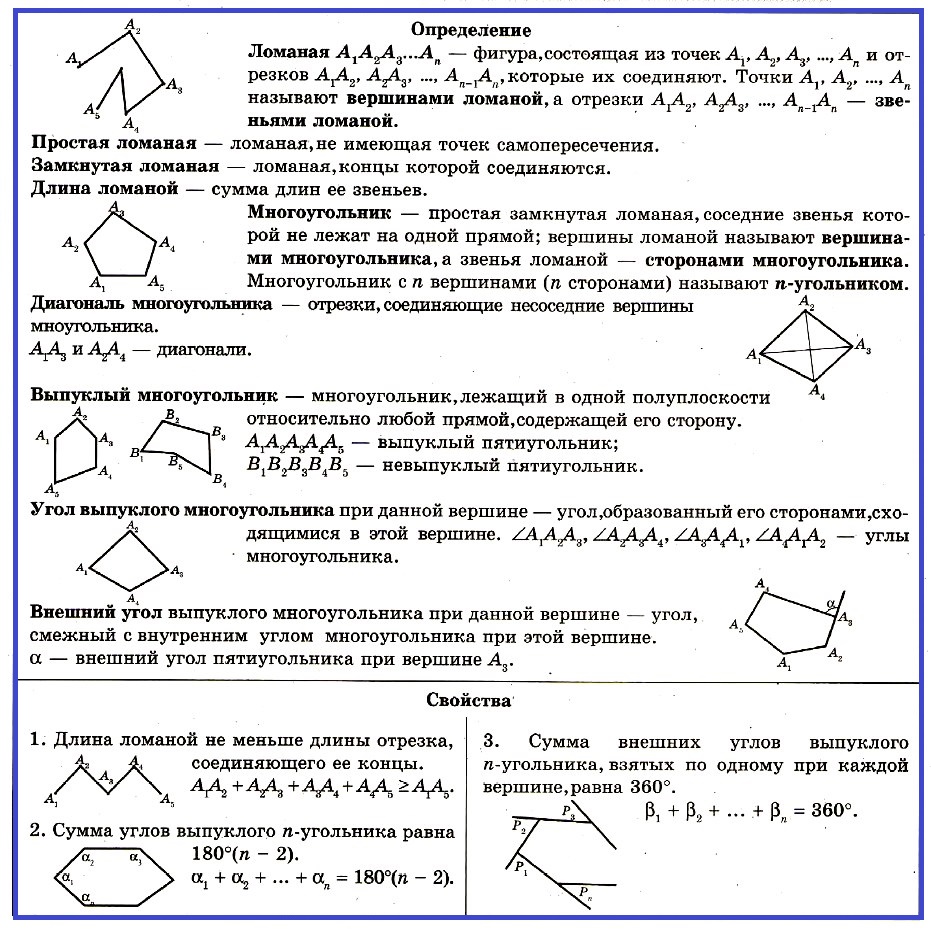
ПРИМЕРЫ РЕШЕНИЯ КЛЮЧЕВЫХ ЗАДАЧ
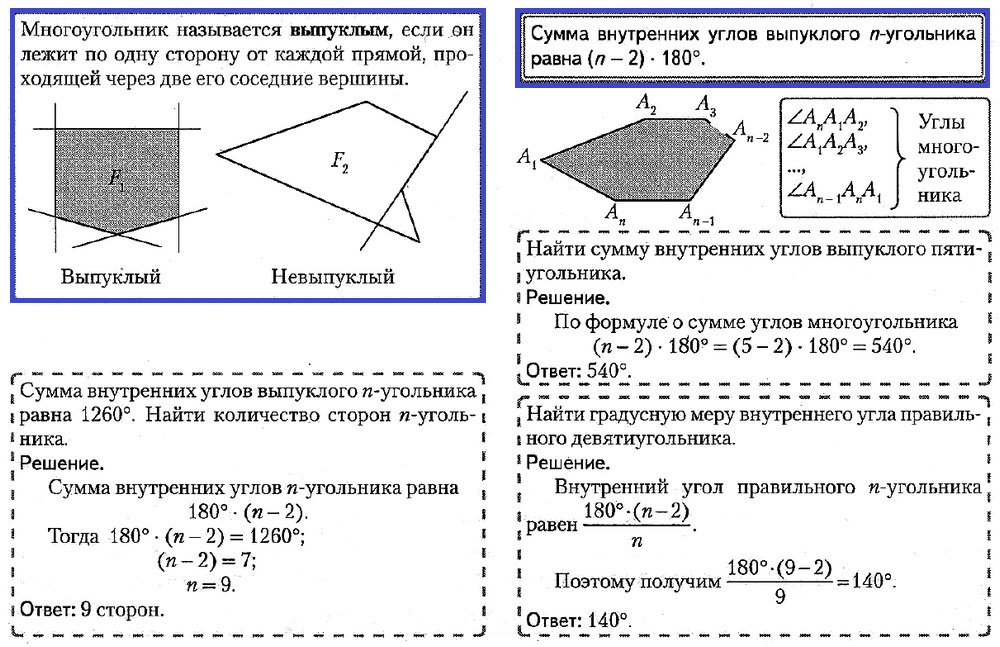
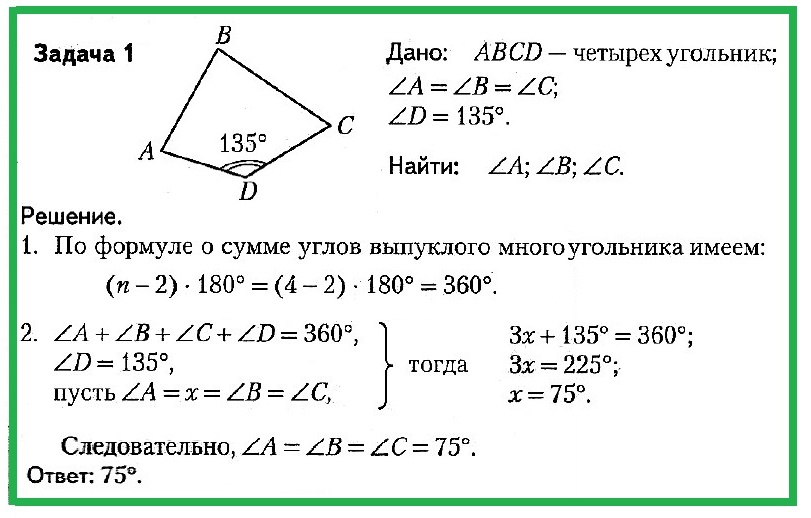
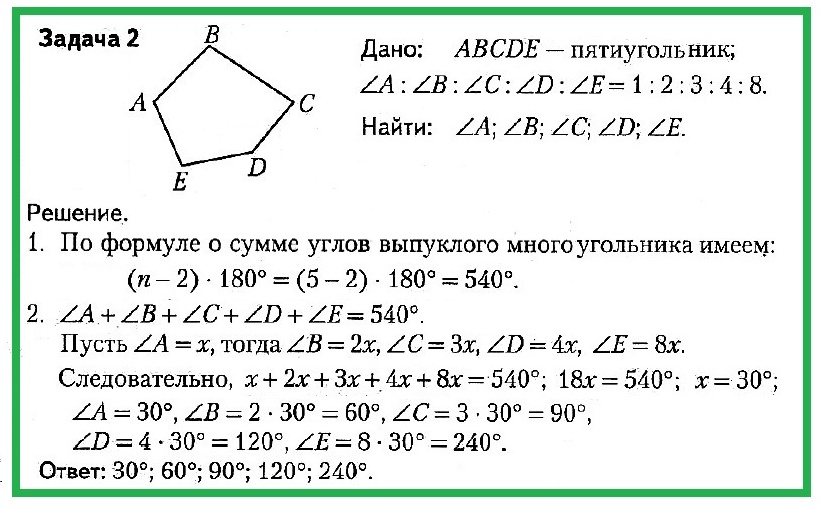
Найти: ∠A, ∠B, ∠C.
Это конспект по теме «Ломаная. Многоугольник + ЗАДАЧИ». Выберите дальнейшие действия:
- Перейти к следующему конспекту: Четырехугольник и его свойства
- Вернуться к Списку конспектов по геометрии