Алгебраические дроби. Сокращение дробей
Алгебраические дроби. Сокращение дробей.
Ключевые слова конспекта: алгебраические дроби, основное свойство дроби, сокращение дробей.
Алгебраической называют дробь, в числителе и (или) знаменателе которой стоят алгебраические выражения. Например:
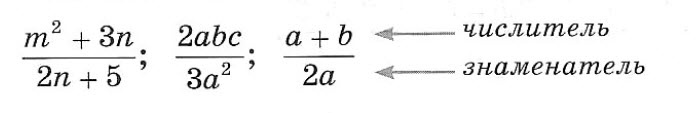
Если в эти выражения вместо букв подставить их числовые значения, то в числителе и знаменателе алгебраической дроби получатся числа, и дробь превратится в обыкновенную. А раз так, то алгебраическая дробь обладает всеми свойствами обыкновенной дроби, в частности основным свойством дроби:
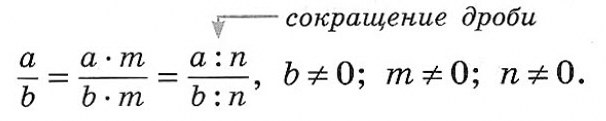
Величина дроби не изменится, если её числитель и знаменатель одновременно умножить или разделить на одно и то же число или алгебраическое выражение, не равное нулю.
Так как на нуль делить нельзя, то сразу договоримся, что знаменатели всех рассматриваемых нами дробей не равны нулю, то есть переменные, из которых состоят знаменатели, принимают только допустимые значения.

Сокращение дробей
Последовательность действий:
- сократить коэффициенты;
- перебрать по очереди все буквы, деля числитель и знаменатель на букву в наименьшей степени (здесь разделили на а2 и на b).
Алгебраические выражения в числителе и знаменателе разложим на множители, полученную дробь сократим:
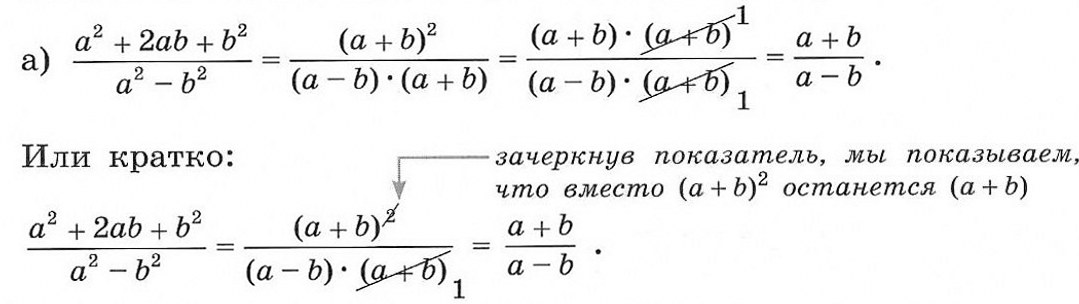
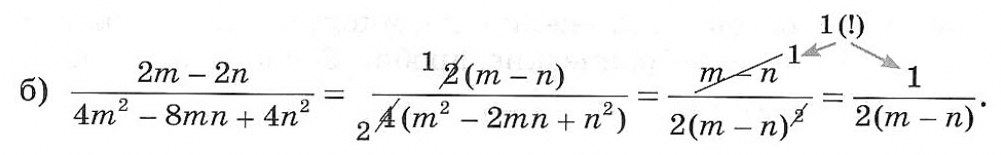
Заметим, что
(а — b) : (а — b) = 1 и (b — а) : (а — b) = — (а — b) : (а — b) = — 1, поэтому
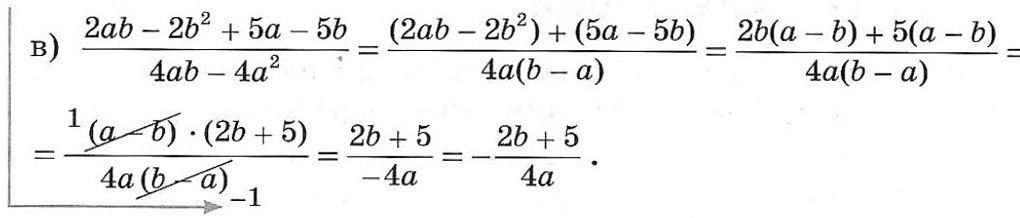
Помни: (а — b)2 = (b — а)2.
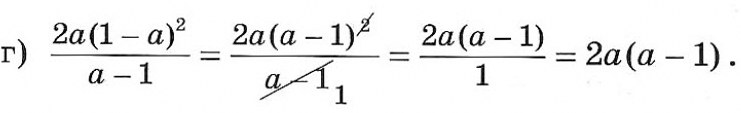
Это конспект по математике на тему «Алгебраические дроби. Сокращение дробей». Выберите дальнейшие действия:
- Перейти к следующему конспекту:
- Вернуться к списку конспектов по Математике.
- Проверить знания по Математике.