Урок 37. Решение задач на применение признаков подобия Δ

Поурочное планирование по геометрии для 8 класса. Ориентировано на работу с УМК Атанасян и др. Геометрия 8 класс. Глава VII. ПОДОБНЫЕ ТРЕУГОЛЬНИКИ. Урок 37. Решение задач на применение признаков подобия треугольников. Вернуться к Списку уроков Тематического планирования.

Урок 37. Решение задач на применение
признаков подобия треугольников

Основные дидактические цели урока: совершенствовать навыки решения задач на применение признаков подобия треугольников; подготовка учащихся к предстоящей контрольной работе.

Ход урока

I. Организационный момент.

Мотивация к учебной деятельности. (Учитель сообщает тему урока, формулирует цели урока.)

II. Анализ ошибок, допущенных в самостоятельной работе

1. Провести общий анализ контрольной работы.
2. Работа над ошибками. (На интерактивной доске записаны готовые ответы и указания к задачам контрольной работы. Учитель делит класс на группы в зависимости от того, какой уровень и вариант самостоятельной работы они выполняли. В одной группе должны быть учащиеся, выполнявшие один и тот же уровень и вариант. Учитель контролирует работу групп и по мере необходимости оказывает помощь.)

Ответы и указания к задачам самостоятельной работы:

I уровень сложности

II уровень сложности

lll уровень сложности

III. Решение задач

Решить задачи № 1—5. (Учитель делит класс на группы и по мере необходимости оказывает индивидуальную помощь.)

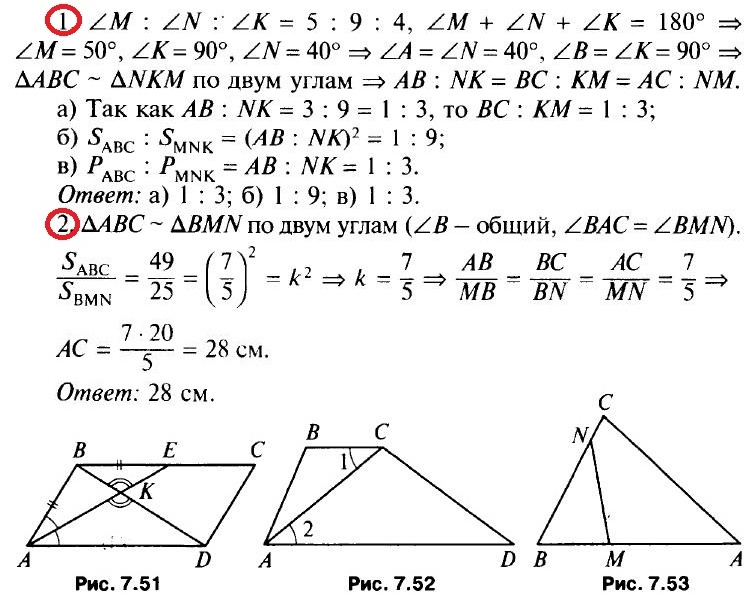
1. В прямоугольном треугольнике ABC ∠A = 40°, ∠B = 90°, а в треугольнике MNK углы М, N, К относятся как 5 : 9 : 4. АВ = 3 см, KN — 9 см. Найдите: а) ВС : КМ; б) S_ABC : S_MNK; в) P_ABC : P_MNK.
2. Дано: MN||АС, S_ABC : S_BMN = 49 : 25, MN = 20 см (рис. 7.50). Найти: АС.
3. В параллелограмме ABCD АЕ — биссектриса угла А. Стороны параллелограмма АВ и ВС относятся как 4 : 9. АЕ пересекает диагональ BD в точке К. Найдите отношение ВК : KD.
4. В трапеции ABCD основания ВС и AD равны 2 и 8 см, а диагональ АС равна 4 см. В каком отношении делит диагональ АС площадь трапеции?
5. Прямая MN пересекает стороны АВ и ВС треугольника АВС в точках М и N соответственно так, что ВС = 2ВМ, АВ = 2BN, ВМ : BN = 3 : 5. Найдите: а) Р_АВС : P_NBM; б) S_ABC : S_NBM; в) MN : АС.

Краткое решение задач (ответы):

IV. Рефлексия учебной деятельности

1. Какие треугольники называются подобными?
2. Сформулируйте признаки подобия треугольников.
3. Чему равно отношение периметров, площадей подобных треугольников?
4. Сформулируйте свойство биссектрисы угла.

Домашнее задание

Решить задачи № 1—3 и дополнительно (по желанию учащихся) задачи № 4—5.

1. Диагонали четырехугольника ABCD АС и BD пересекаются в точке О так, что ОС = 5 см, ОВ = 6 см, ОА = 15 см, OD = 18 см. Докажите, что в четырехугольнике ABCD ВС||AD и найдите отношение треугольников AOD и ВОС.
2. Перпендикулярно высоте BD треугольника АВС проведена прямая, пересекающая стороны АВ и ВС в точках М и Р соответственно. Найдите АВ и отношение площадей треугольников МРВ и АВС, если известно, что ВМ = 7 см, ВР = 9 см, PC = 18 см.
3. Прямая EF пересекает стороны АВ и ВС треугольника АВС в точках Е и F соответственно так, что ∠A + ∠EFC = 180°, а площадь четырехугольника AEFC относится к площади треугольника EBF как 16 : 9. Докажите, что треугольник BFE подобен треугольнику ВАС и найдите коэффициент подобия данных треугольников.
4. Диагональ BD четырехугольника ABCD является биссектрисой его угла, ВС • ВА = ВD². Докажите, что ∠BAD = ∠BDC. В каком отношении площадь четырехугольника делится его диагональю BD, если известно, что DC : AD = 3 : 2?
5. На стороне АС треугольника АВС отмечена точка К так, что ΔАВК ~ ΔАВС. Найдите АК, КС, ВК, если известно, что АВ : ВС : АС = 3 : 7 : 9, а периметр треугольника АВС равен 57 см.

Вы смотрели: Поурочное планирование по геометрии для 8 класса. УМК Атанасян и др. (Просвещение). Глава VII. ПОДОБНЫЕ ТРЕУГОЛЬНИКИ. Урок 37. Решение задач на применение признаков подобия треугольников.

Вернуться к Списку уроков Тематического планирования.