Урок 35. 2-й и 3-й признаки подобия треугольников

Поурочное планирование по геометрии для 8 класса. Ориентировано на работу с УМК Атанасян и др. Геометрия 8 класс. Глава VII. ПОДОБНЫЕ ТРЕУГОЛЬНИКИ. Урок 35. Второй и третий признаки подобия треугольников. Вернуться к Списку уроков Тематического планирования.

Урок 35. Второй и третий признаки
подобия треугольников

Основные дидактические цели урока: рассмотреть второй и третий признаки подобия треугольников; показать применение второго и третьего признаков подобия треугольников при решении задач.

Ход урока

I. Организационный момент.

Мотивация к учебной деятельности. (Учитель сообщает тему урока, формулирует цели урока.)

II. Актуализация знаний учащихся

1. Работа в рабочих тетрадях.

Решить задачу № 57 (самостоятельно с последующим обсуждением решения).

Наводящие вопросы.

• Докажите, что ΔABF ~ ΔCDF.
• Чему равен коэффициент подобия треугольников ABF и CDF?
• Найдите отношение сторон BF и DF.
• Чему равно значение DF?

2. Решение задач по готовым чертежам (самостоятельно). (В тетрадях записать краткое решение.)

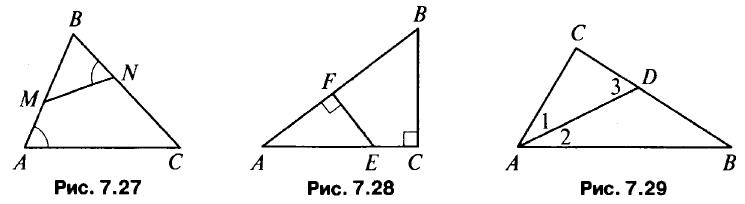
• 1) Дано: ∠N = ∠A, ВС = 12 см, MN = 6 см, CN = 4 см (рис. 7.27). Найти: АС.
• 2) Дано: ВС ⊥ АС, EF ⊥ AB, ВС = 12 см, EF = 6 см, АЕ = 10 см (рис. 7.28). Найти: АВ.
• 3) Дано: ∠3 = ∠1 + ∠2, CD = 4 см, ВС = 9 см (рис. 7.29). Найти: АС.

3. Обсуждение решений задач, с которыми не справилось большинство учащихся.

III. Работа по теме урока

1. Формулировка темы урока.

• Сформулируйте первый признак равенства треугольников.
• Существуют ли еще какие-либо признаки подобия треугольников?

2. Сформулировать другие признаки подобия треугольников (работа в группах).
3. Доказать второй и третий признаки подобия треугольников.

Второй признак подобия треугольников

Теорема: Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, заключенные между этими сторонами, равны, то такие треугольники подобны.

(Учащиеся записывают в тетрадях план-конспект доказательства теоремы.)

План-конспект доказательства теоремы

4. Составить план-конспект доказательства третьего признака подобия треугольников. (Учитель делит класс на группы. На обсуждение дается 5 мин. Далее заслушивают представителей групп, в обсуждении решения участвует весь класс.)

Третий признак подобия треугольников

Теорема: Если три стороны одного треугольника пропорциональны трем сторонам другого треугольника, то такие треугольники подобны.

План-конспект доказательства теоремы

IV. Закрепление изученного материала

1. Работа в рабочих тетрадях.

Решить задачи № 59, 60 (работа в парах). (Учитель контролирует работу менее подготовленных учащихся и по мере необходимости оказывает индивидуальную помощь.)

Задача № 59. Наводящие вопросы.

• Каким является ∠C для треугольников АВС и MNC?
• Чему равно отношение сторон, заключающих этот угол (АС : CN и ВС : СМ)?
• Что можно сказать о сторонах АС и ВС треугольника АВС и сторонах CN и СМ треугольника MNC?
• Какой признак подобия треугольников был применен при доказательстве подобия треугольников MNC и АВС?

Задача № 60. Наводящие вопросы.

• Чему равно отношение сторон MN и CD, МР и СЕ, NP и DE треугольников MNP и CD ЕР
• Что можно сказать о сторонах треугольников MNP и CDE?
• Укажите признак, на основании которого треугольники MNP и CDE подобны.

(Учащиеся, успешно справившиеся с решением задач, решают дополнительные задачи.)

2. Решить дополнительные задачи.

1) В треугольниках АВС и А₁В₁С₁, BE и В₁Е₁ — биссектрисы, ∠B = ∠B₁, АЕ : ЕС = А₁Е₁ : Е₁С₁. Докажите, что ΔАВЕ ~ ΔА₁В₁Е₁.

2) В треугольнике АВС АВ = 4, ВС = 6, АС = 7. Точка Е лежит на стороне АВ. Внутри треугольника взята точка М так, что МВ = 5,25, ME = 4,5, АЕ = 1. Прямая ВМ пересекает АС в точке Р. Докажите, что ΔАРВ равнобедренный.

V. Рефлексия учебной деятельности

1. Сформулируйте второй (третий) признак подобия треугольников.
2. Две стороны одного треугольника пропорциональны двум сторонам другого. В каком случае данные треугольники будут подобны?
3. Подобны ли равнобедренные треугольники, если у них углы между боковыми сторонами равны?
4. Подобны ли равнобедренные треугольники, если боковая сторона и основание одного из них пропорциональны боковой стороне и основанию другого?
5. Могут ли быть подобными прямоугольные треугольники, если катеты одного из них пропорциональны катетам другого?

Домашнее задание

1. П. 62, 63, вопросы 6, 7 (учебник, с. 158, 159).
2. Решить задачи № 559, 560 (б), 561.
3. Решить дополнительную задачу.

В треугольниках ABС и A₁B₁C₁, BD и B₁D₁ — медианы, ∠A = ∠A₁, ∠BDA = ∠В₁D₁A₁. Докажите, что треугольник BDC подобен треугольнику B₁D₁С₁.

Вы смотрели: Поурочное планирование по геометрии для 8 класса. УМК Атанасян и др. (Просвещение). Глава VII. ПОДОБНЫЕ ТРЕУГОЛЬНИКИ. Урок 35. Второй и третий признаки подобия треугольников.

Вернуться к Списку уроков Тематического планирования.