Статистические характеристики
Статистические характеристики
Ключевые слова конспекта: статистические характеристики, статистические исследования, выборка, варианта, объем выборки, среднее арифметическое, вариационный ряд, размах ряда, мода выборки, медиана ряда.
Статистические исследования
Для изучения, обработки и анализа количественных данных различных массовых социально-экономических процессов и явлений проводят статистические (от латинского слова status — «состояние, положение вещей») исследования. Уже в древних государствах вели учёт населения, способного платить налоги. С развитием общества потребовались научные методы обработки и анализа самых разнообразных сведений. Так, в XIX в. появилась биологическая статистика, названная биометрикой и изучающая численные характеристики отдельных биологических особей и их популяций. Можно назвать ещё более десятка различных статистик: экономическая, финансовая, налоговая, демографическая, медицинская, метеорологическая и т. д.
Каждое статистическое исследование состоит из сбора и обработки информации. На основе полученных данных составляются различные прогнозы, оценивается их достоверность и т.д. Важной задачей, без которой статистические данные теряют всякий смысл, является обработка полученных данных.
Рассмотрим пример. Учащимся двух седьмых классов был предложен тест по математике, состоящий из 10 заданий. При проверке работ отмечали количество заданий, верно выполненных учащимися. Получили два ряда чисел:
7 «А» класс: 8; 7; 2; 5; 10; 9; 8; 7; 7; 10; 9; 6; 5; 8; 8; 10; 9; 9; 10; 7; 9; 10; 7; 9; 6;
7 «Б» класс: 8; 7; 8; 6; 9; 9; 7; 8; 7; 9; 9; 6; 5; 8; 7; 10; 9; 10; 10; 7; 8; 9; 7; 9; 9.
Ряд данных, полученных в результате статистического исследования, называют выборкой, а каждое число этого ряда — вариантой выборки. Количество чисел в ряду называют объёмом выборки. В нашем примере объёмом выборки является количество учащихся каждого класса, участвовавших в тестировании. В каждом случае объём выборки равен 25.
Имея приведённые выше два ряда данных, трудно сравнить результаты выполнения теста учащимися двух классов. А если рассматривать результаты, которые показали все семиклассники города или целого региона, то информация будет столь громоздкой, что окажется бесполезной. Потому для статистической обработки данных рассматривают различные статистические характеристики.
Среднее арифметическое. Вариационный ряд
Одной из характеристик, широко применяемых в статистических исследованиях, является среднее арифметическое.
✅ Определение. Средним арифметическим ряда данных называется частное суммы всех вариант ряда и количества вариант.
Поскольку количество вариант — это объём выборки, то среднее арифметическое выборки есть частное суммы всех вариант и объёма выборки.
Рассмотрим пример. Найдём средний балл, который получили учащиеся 7 «А» класса при выполнении теста:
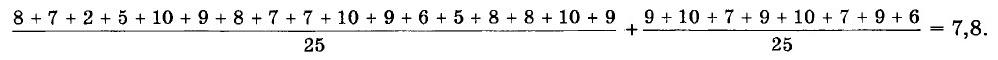
Такой подсчёт среднего арифметического выборки не очень удобен. Можно поступать иначе. Перепишем выборку для 7 «А» класса, расположив её варианты так, чтобы каждая следующая была не меньше предыдущей. Получим:
2; 5; 5; 6; 6; 7; 7; 7; 7; 7; 8; 8; 8; 8; 9; 9; 9; 9; 9; 9; 10; 10; 10; 10; 10.
Такую запись выборки называют упорядоченным рядом данных (или вариационным рядом). Теперь легко видеть, что 2 балла получил один ученик, 5 баллов — два ученика, 6 баллов — два ученика, 7 баллов — пять учеников и т.д. Количество появлений одной и той же варианты в выборке называют частотой этой варианты. Так, например, частота варианты 7 равна 5, частота варианты 10 равна 5. Составим таблицу частот вариант для учащихся 7 «А» класса. В первой строке запишем все возможные количества баллов, которые могли получить учащиеся при выполнении теста, т.е. числа от 0 до 10. Во второй строке запишем соответствующие частоты, т.е. число учащихся, получивших указанное количество баллов.
Проверим, не ошиблись ли мы при подсчёте частот: сумма частот должна быть равна объёму выборки. Действительно, 0 + 0 + 1+ 0 + 0 + 2 + 2 + 5 + 4 + 6 + 5 = 25 (естественно, нули можно не писать). Теперь можно вычислить среднее арифметическое выборки проще: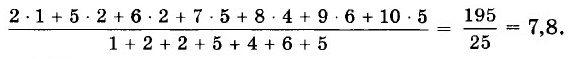
Заметим, что среднее арифметическое упорядоченного ряда данных и среднее арифметическое выборки — одно и то же число. Составим таблицу частот выборки для 7 «Б» класса.
Заметим, что обычно в таблицу частот не включают варианты, частоты которых равны нулю. В этом случае таблица частот для 7 «Б» класса будет такой:
Найдём объём выборки: 1 + 2 + 6 + 5 + 8 + 3 = 25. Теперь найдём среднее арифметическое:
![]()
Зная средние баллы учащихся 7 «А» и 7 «Б» классов, можно сделать вывод, что учащиеся 7 «Б» в целом выполнили тест лучше, поскольку 8,04 > 7,8.
Составленные таблицы частот позволяют сделать и другие полезные выводы по итогам проведённого тестирования. Например, для первой выборки (результаты учащихся 7 «А» класса) наименьший полученный балл равен 2, наибольший — 10. Результаты всех учащихся класса располагаются между этими числами. Для второй выборки наименьшая варианта равна 5, наибольшая — 10. Это может означать, что 7 «Б» класс по своей математической подготовке является более однородным, чем 7 «А».
Размах ряда. Мода выборки
Ещё одним показателем, который используется при анализе статистических данных, является размах ряда.
✅ Определение. Разность наибольшей и наименьшей вариант выборки называют размахом ряда.
В рассмотренном ранее примере размах первой выборки (или упорядоченного ряда данных) равен 10 — 2 = 8, а второй 10-5 = 5. Размах выборки находят в том случае, когда существенной для исследования является величина разброса данных в ряду. К примеру, в метеорологии важна не только среднесуточная температура, но и численная характеристика колебания температуры воздуха в течение суток, т. е. размах выборки.
Заметим, что на практике при анализе данных, полученных в результате исследования, бывает удобно использовать ещё одну статистическую характеристику — так называемую моду выборки.
✅ Определение. Варианта выборки, имеющая наибольшую частоту, называется модой выборки.
В рассмотренном примере с изучением результатов тестирования, проведённого в двух седьмых классах, модой и первого, и второго ряда является число 9, которое и в первой, и во второй выборке встречается чаще других.
Моду ряда находят тогда, когда нужно выявить типичный для данной выборки показатель. Если, например, изучаются данные о размерах мужских рубашек, проданных в магазине в определённый день, то удобно бывает воспользоваться таким показателем, как мода, который характеризует размер, пользующийся наибольшим спросом.
Если в выборке два числа встречаются с одинаковой частотой, превосходящей частоты, с которыми встречаются другие числа, то обе эти варианты являются модой для данного ряда. Так, в ряду 2; 3; 3; 3; 5; 5; 6; 6; 6; 7; 8; 8 две моды — это числа 3 и 6. Может случиться, что в выборке будет более двух мод или не будет моды совсем. Например, ряд 2; 2; 3; 3; 4; 4; 5; 5 не имеет моды.
Медиана ряда
Ещё одной характеристикой, используемой в статистике, является медиана ряда.
Рассмотрим пример. Сотрудники лаборатории приобрели акции одного предприятия. Количество акций, приобретённых сотрудниками, оказалось таким: 2; 3; 5; 6; 8; 9; 51. Нужно оценить среднее количество приобретённых акций.
Данный ряд не имеет моды. Найдём среднее арифметическое ряда:![]()
Найденное число не отражает реальной ситуации с распределением акций между сотрудниками лаборатории, поскольку оно больше шести из семи вариант ряда. Для оценки средней величины поступим иначе. Составим из полученных данных упорядоченный ряд и найдём варианту, записанную в середине ряда.
2; 3; 5; 6; 8; 9; 51.
Эту варианту называют медианой. Она равна 6. Естественно, найденное значение лишь приближённо характеризует средний показатель ряда, однако эта характеристика ближе к действительности.
Если ряд имеет чётное число вариант, то в качестве медианы рассматривают среднее арифметическое двух средних элементов. Например, медианой ряда 3; 3; 4; 5; 5: 6: 6; 7; 7; 40 является среднее арифметическое чисел 5 и 6, т.е. (5 + 6)/2 = 5,5.
✅ Определение. Если в упорядоченном ряду данных нечётное число вариант, то средняя по счёту варианта называется медианой ряда. Если в упорядоченном ряду чётное число вариант, то среднее арифметическое двух средних по счёту вариант называется медианой ряда.
Медианой произвольной выборки является медиана соответствующего упорядоченного ряда. Заметим, что если упорядоченный ряд данных содержит 2n — 1 вариант (n — натуральное число), то медианой является n-я варианта, а если упорядоченный ряд данных содержит 2n чисел, то медианой является среднее арифметическое n-го и n + 1-го чисел.
Рассмотрим пример. Во время соревнований по стрельбе спортсмен набрал следующее количество очков: 9; 9; 8; 10; 8; 7; 9; 10; 8; 7. Найдём: а) объём выборки; б) среднее арифметическое выборки; в) размах; г) моду ряда; д) медиану выборки.
Для решения задачи запишем упорядоченный ряд данных:
7; 7; 8; 8; 8; 9; 9; 9; 10; 10.
а) Спортсмен сделал 10 выстрелов, значит, объём выборки равен 10.
б) Найдём среднее арифметическое выборки![]()
в) Размах ряда равен 10 — 7 = 3.
г) У данного ряда две моды: 8 и 9.
д) Найдём медиану выборки. Данный ряд содержит чётное число вариант. Найдём среднее арифметическое двух чисел, записанных в середине ряда: (8 + 9)/2 = 8,5. Медианой выборки является число 8,5.
Это конспект по математике на тему «Статистические характеристики». Выберите дальнейшие действия:
- Перейти к следующему конспекту:
- Вернуться к списку конспектов по Математике.
- Проверить знания по Математике.