Решение задач: Исполнители алгоритмов
Решение задач: Исполнители алгоритмов
Ключевые слова: типовые задачи по теме Исполнители алгоритмов — «Калькулятор», «Черепашка», «Робот», «Кузнечик», «Бусины», «Цепочки», «Камешки», решение задач, ответы на задачи.
1. Решение задач по теме «Калькулятор»
Задача № 1.[/su_highlight] У исполнителя Калькулятор две команды, которым присвоены номера:
- вычти 1;
- умножь на 3.
Первая из них уменьшает число на экране на 1, вторая — увеличивает его в 3 раза. Запишите порядок команд в программе получения из 4 числа 17, содержащей не более 5 команд, указывая лишь номера команд. Например, 12211 — это программа:
вычти 1;
умножь на 3;
умножь на 3;
вычти 1;
вычти 1,
которая преобразует число 2 в 7. Если таких программ более одной, то запишите любую из них.
Задача № 2.[/su_highlight] У исполнителя Калькулятор две команды, которым присвоены номера:
- возведи в квадрат;
- вычти 1.
Первая из них возводит число на экране в квадрат, вторая уменьшает его на 1. Запишите порядок команд в программе получения из числа 5 числа 8, содержащей не более 4 команд, указывая лишь номера команд. Например, программа 12122 — это программа:
возведи в квадрат;
вычти 1;
возведи в квадрат;
вычти 1;
вычти 1,
которая преобразует число 2 в 7.
Задача № 3.[/su_highlight] У исполнителя Утроитель две команды, которым присвоены номера:
- прибавь 1;
- умножь на 3.
Первая из них увеличивает число на экране на 1, вторая — утраивает его. Программа для Утроителя — это последовательность команд. Сколько есть программ, которые число 1 преобразуют в число 29? Ответ обоснуйте.
2. Решение задач по теме «Черепашки»
Задача № 4.[/su_highlight]
Исполнитель Черепашка перемещается на экране компьютера, оставляя след в виде линии. В каждый конкретный момент известно положение исполнителя и направление его движения. У исполнителя существуют две команды:
- Вперед n, где n — целое число, вызывающая передвижение черепашки на n шагов в направлении движения;
- Направо m, где m — целое число, вызывающая изменение направления движения на m градусов по часовой стрелке.
Запись Повтори 5 [Команда1 Команда2] означает, что последовательность команд в скобках повторится 5 раз. Исполнитель интерпретирует эту запись как одну команду. Черепашке был дан для исполнения следующий алгоритм:
Повтори 5 [Повтори 2 [Вперед 40 Направо 60 Вперед 40 Направо 120] Направо 90]
Какая фигура появится на экране?

Задача № 5.[/su_highlight] Исполнитель Черепашка перемещается на экране компьютера, оставляя след в виде линии. В каждый конкретный момент известно положение исполнителя и направление его движения. У исполнителя существуют три команды:
- Вперед n, где n — целое число, вызывающая передвижение черепашки на n шагов в направлении движения;
- Направо m, где m — целое число, вызывающая изменение направления движения на m градусов по часовой стрелке;
- Налево m, где m — целое число, вызывающая изменение направления движения на m градусов против часовой стрелки.
Запись Повтори 5 [Команда1 Команда2] означает, что последовательность команд в квадратных скобках повторится 5 раз. Черепашке был дан для исполнения следующий алгоритм:
Повтори 5 [Вперед 30 Налево 72]
Какая фигура появится на экране? Где будет находиться эта фигура по отношению к Черепашке?
3. Решение задач по теме «Робот»
Задача № 6.[/su_highlight] Исполнитель Робот действует на клетчатой доске, между соседними клетками которой могут стоять стены. Робот передвигается по клеткам доски и может выполнять команды 1 (вверх), 2 (вниз), 3 (вправо), 4 (влево), переходя на соседнюю клетку в направлении, указанном в скобках. Если в этом направлении между клетками стоит стена, то Робот разрушается. Робот успешно выполнил программу
11313142
Какую последовательность из четырех команд должен выполнить Робот, чтобы вернуться в ту клетку, где он был перед началом выполнения программы, и не разрушиться вне зависимости от того, какие стены стоят на поле?
4. Решение задач по теме «Кузнечик»
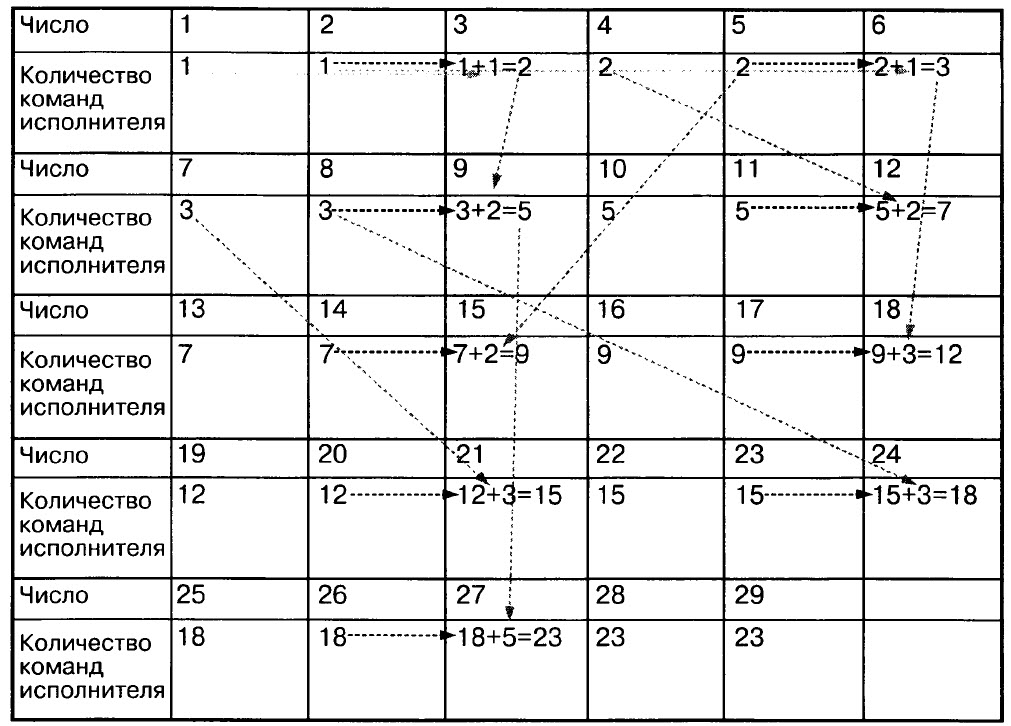
Задача № 7.[/su_highlight] Имеется исполнитель Кузнечик, который живет на числовой оси. Система команд Кузнечика: “Вперед ЛГ (Кузнечик прыгает вперед на N единиц); “Назад М’ (Кузнечик прыгает назад на М единиц). Переменные N и М могут принимать любые целые положительные значения. Известно, что Кузнечик выполнил программу из 51 команды, в которой команд “Назад 2” в 2 раза больше, чем команд “Вперед 3”. Других команд в программе не было. На какую одну команду можно заменить эту программу, чтобы Кузнечик оказался в той же точке, что и после выполнения программы?
5. Решение задач по теме «Бусины»
Задача № 8.[/su_highlight] Цепочка из трех бусин формируется по следующему правилу: На первом месте в цепочке стоит одна из бусин М, Н, О. На втором — одна из бусин Л, М, О. На третьем месте — одна из бусин Л, М, Н, не стоящая в цепочке на первом или втором месте. Какая из следующих цепочек создана по этому правилу:
1) НОН 2) НОМ 3) МНЛ 4) МНО.
6. Решение задач по теме «Цепочки»
Задача № 9.[/su_highlight] Цепочки символов (строки) создаются по следующему правилу.
Первая строка состоит из одного символа — цифры «1».
Каждая из последующих цепочек создается следующим действием: в очередную строку дважды записывается предыдущая цепочка цифр (одна за другой, подряд), а в конец приписывается еще одно число — номер строки по порядку (на i-м шаге дописывается число «i»).
Вот первые 4 строки, созданные по этому правилу:
1) 1
2) 112
3) 1121123
4) 112112311211234
Сколько раз в общей сложности встречаются в седьмой строке нечетные цифры (1, 3, 5, 7, 9)?
7. Решение задач по теме «Камешки«
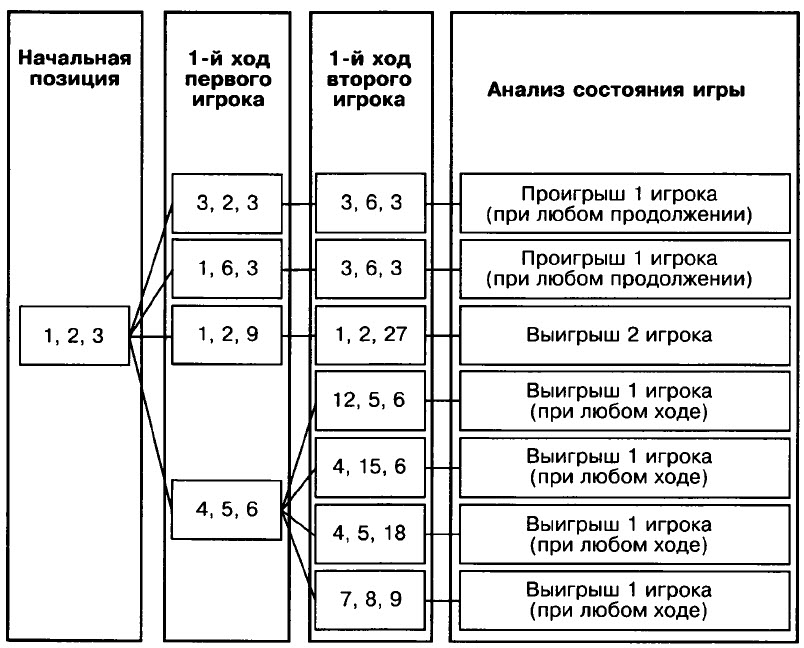
Задача № 10.[/su_highlight] Два игрока играют в следующую игру.
Имеются три кучи камней, содержащих соответственно 1,2,3 камня. За один ход разрешается или утроить количество камней в какой-нибудь куче, или добавить по 3 камня в каждую из трех куч. Предполагается, что у каждого игрока имеется неограниченный запас камней.
Выигрывает тот игрок, после хода которого в какой-нибудь куче становится больше 20 камней или во всех трех кучах суммарно становится не менее 30 камней.
Игроки ходят по очереди. Выяснить, кто выигрывает при правильной игре, — первый или второй игрок.
Конспект урока по информатике «Решение задач: Исполнители алгоритмов».
Вернуться к Списку конспектов по информатике.
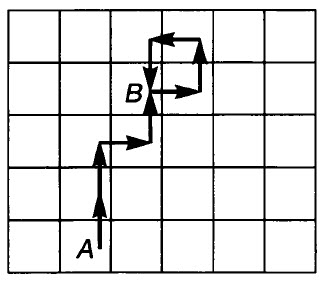 Решение: Начертим траекторию, по которой двигался Робот. Начальную точку движения обозначим буквой Л, конечную — В. Из рисунка видно, что вернуться из точки В в точку А можно по программе из четырех команд: вниз, влево, вниз, вниз, т. е. 2422.
Решение: Начертим траекторию, по которой двигался Робот. Начальную точку движения обозначим буквой Л, конечную — В. Из рисунка видно, что вернуться из точки В в точку А можно по программе из четырех команд: вниз, влево, вниз, вниз, т. е. 2422.