Опорный конспект 3. Теорема синусов. Теорема косинусов
Теорема синусов. Теорема косинусов
Наглядная геометрия 9 класс. Опорный конспект 3. Теорема синусов. Теорема косинусов
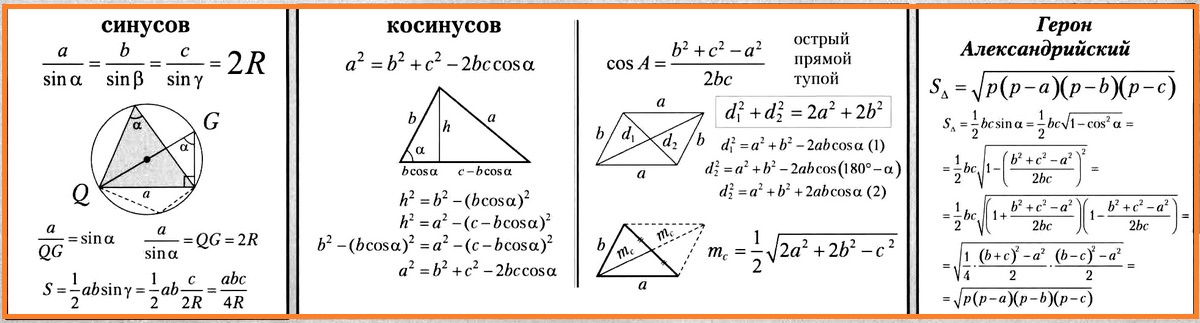
Есть в курсе геометрии две очень важные теоремы, связанные с синусом и косинусом угла треугольника. Они так и называются: Теорема синусов и Теорема косинусов.
Теорема синусов вам, в принципе, уже знакома по 1-му и 2-му конспектам: «Отношение стороны треугольника к синусу противолежащего угла есть величина постоянная: a / sin α = 2R».
Теорема косинусов позволяет, зная две стороны и угол между ними, найти третью сторону треугольника. Звучит она достаточно длинно: «Квадрат любой стороны треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон на косинус угла между ними». В виде формулы теорема выглядит уже проще: a2 = b2 + с2 – 2bc cos α. Запоминается она легко.
Из теоремы косинусов вытекают многочисленные следствия, которые часто используются при решении задач. Можно смело сказать, что это самая работающая теорема. Из нее, в частности, следует и теорема Пифагора: если α = 90°, то cos 90° = 0, тогда а2 = b2 + с2.
При помощи теоремы косинусов можно вывести красивую формулу площади треугольника по трем сторонам. Это формула Герона:![]()
где а, b и с — стороны треугольника, а р = (a + b + c)/2 — полупериметр. Измерили три стороны треугольника линейкой и при помощи формулы нашли его площадь. Здорово?! А вот формулу Герона открыл не Герон, а Архимед. Но ее назвали в честь Герона. В науке так бывает.
ТАБЛИЦА «Теорема синусов. Теорема косинусов»

1. Теорема синусов.
Теорема синусов. Стороны треугольника пропорциональны синусам противолежащих углов.
Доказательство. Дан треугольник со стороной а и противолежащим углом α. Опишем вокруг треугольника окружность. Из конца хорды а проведем диаметр QG. Так как угол, опирающийся на диаметр, — прямой, то получим прямоугольный треугольник с гипотенузой QG и острым углом α (углы, опирающиеся на одну и ту же дугу, равны).![]()
Точно так же доказываем, что![]()
Следовательно,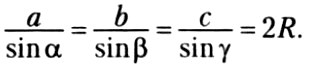
* Для тупого угла (180° – α) по формуле приведения![]()
2. Формула нахождения радиуса R описанной окружности.
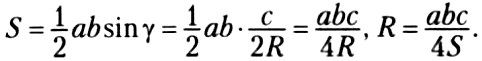
3. Теорема косинусов.
Теорема косинусов. Квадрат любой стороны треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон на косинус угла между ними: а2 = b2 + с2 – 2bc cos α.
Доказательство. Проекция стороны b на сторону с равна b cos α. Проекция стороны а на сторону с равна с – b cos α. Из левого прямоугольного треугольника h2 = b2 – (b cos α)2, из правого h2 = а2 – (с – b cos α)2. Приравняем правые части равенств: b2 – (b cos α)2 = а2 – с2 + 2bc cos α – (b cos α)2, откуда a2 = b2 + c2 – 2bc cos α.
4. Нахождение косинуса угла треугольника по трем сторонам.
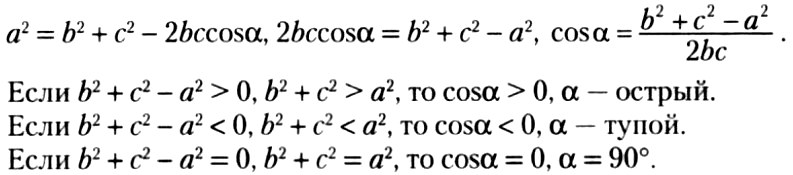
5. Теорема о сумме квадратов диагоналей параллелограмма.
Теорема. Сумма квадратов диагоналей параллелограмма равна сумме квадратов всех его четырех сторон.

6. Формула медианы треугольника.

7. Формула Герона.

ЭТО НУЖНО ЗНАТЬ !

Это опорный конспект № 3 по геометрии для 9 класса «Теорема синусов. Теорема косинусов». Выберите дальнейшие действия:
- Вернуться к Списку конспектов по геометрии
- Смотреть Опорный конспект 1. Окружности
- Смотреть Опорный конспект 2. Описанные и вписанные окружности
- Смотреть Опорный конспект 4. Правильные многоугольники