Ключевые слова конспекта: Натуральные числа. Арифметические действия над натуральными числами. Делимость натуральных чисел. Простые и составные числа. Разложение натурального числа на простые множители. Признаки делимости на 2, 3, 5, 9, 4, 25, 10, 11. Наибольший общий делитель (НОД), а также наименьшее общее кратное (НОК). Деление с остатком.

Натуральные числа — это числа, которые используются для счета предметов — 1, 2, 3, 4, … Но число 0 не является натуральным!

Множество натуральных чисел обозначают N. Запись «3 ∈ N» означает, что число три принадлежит множеству натуральных чисел, а запись «0 ∉ N» означает, что число нуль не принадлежит этому множеству.

Десятичная система счисления — позиционная система счисления по основанию 10.

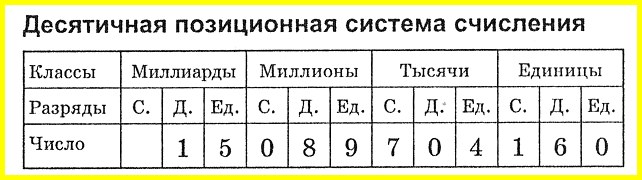
Арифметические действия над натуральными числами

Для натуральных чисел определены следующие действия: сложение, вычитание, умножение, деление, возведение в степень, извлечение корня. Первые четыре действия являются арифметическими.

Пусть a, b и c — натуральные числа, тогда

1. СЛОЖЕНИЕ. Слагаемое + Слагаемое = Сумма

Свойства сложения
1. Переместительное а + b = b + а.
2. Сочетательное а + (b + с) = (а + b) + с.
3. а + 0= 0 + а = а.

2. ВЫЧИТАНИЕ. Уменьшаемое — Вычитаемое = Разность

Свойства вычитания
1. Вычитание суммы из числа а — (b + с) = а — b — с.
2. Вычитание числа из суммы (а + b) — с = а + (b — с); (а + b) — с = (а — с) + b.
3. а — 0 = а.
4. а — а = 0.

3. УМНОЖЕНИЕ. **Множитель * Множитель = Произведение**

Свойства умножения
1. Переместительное а*b = b*а.
2. Сочетательное а*(b*с) = (а*b)*с.
3. 1 * а = а * 1 = а.
4. 0 * а = а * 0 = 0.
5. Распределительное (а + b) * с = ас + bс; (а — b) * с = ас — bс.

4. ДЕЛЕНИЕ. Делимое : Делитель = Частное

Свойства деления
1. а : 1 = а.
2. а : а = 1. Делить на ноль нельзя!
3. 0 : а= 0.

Порядок действий

1. Прежде всего действия в скобках.
2. Потом умножение, деление.
3. И только в конце сложение, вычитание.

Делимость натуральных чисел. Простые и составные числа.

Делителем натурального числа а называется натуральное число, на которое а делится без остатка. Число 1 является делителем любого натурального числа.

Натуральное число называется простым, если оно имеет только два делителя: единицу и само это число. Например, числа 2, 3, 11, 23 — простые числа.

Число, имеющее более двух делителей, называется составным. Например, числа 4, 8, 15, 27 — составные числа.

Признак делимости произведения нескольких чисел: если хотя бы один из множителей делится на некоторое число, то и произведение делится на это число. Произведение 24 • 15 • 77 делится на 12, поскольку множитель этого числа 24 делится на 12.

Признак делимости суммы (разности) чисел: если каждое слагаемое делится на некоторое число, то и вся сумма делится на это число. Если а : b и c : b, то (а + c) : b. А если а : b, а c не делится на b, то a + c не делится на число b.

Если а : c и c : b, то а : b. Исходя из того, что 72 : 24 и 24 : 12, делаем вывод, что 72 : 12.

Представление числа в виде произведения степеней простых чисел называют разложением числа на простые множители.

Основная теорема арифметики: любое натуральное число (кроме 1) либо является простым, либо его можно разложить на простые множители только одним способом.

При разложении числа на простые множители используют признаки делимости и применяют запись «столбиком» В таком случае делитель располагается справа от вертикальной черты, а частное записывают под делимым.

Например, задание: разложить на простые множители число 330. Решение:

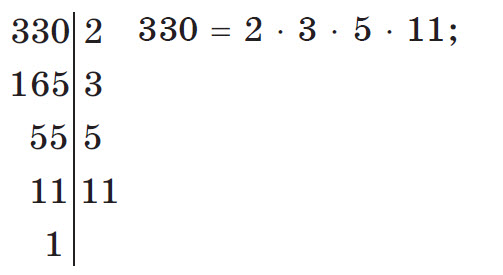
Признаки делимости на 2, 5, 3, 9, 10, 4, 25 и 11.

Существуют признаки делимости на 6, 15, 45 и т. д., то есть на числа, произведение которых можно разложить на множители 2, 3, 5, 9 и 10.

Наибольший общий делитель

Наибольшее натуральное число, на которое делится нацело каждое из двух данных натуральных чисел, называется наибольшим общим делителем этих чисел (НОД). Например, НОД (10; 25) = 5; а НОД (18; 24) = 6; НОД (7; 21) = 1.

Если наибольший общий делитель двух натуральных чисел равен 1, то эти числа называются взаимно простыми.

Алгоритм нахождения наибольшего общего делителя (НОД)

[idea]НОД часто используется в задачах. Например, между учениками одного класса поделили поровну 155 тетрадей и 62 ручки. Сколько учеников в этом классе?

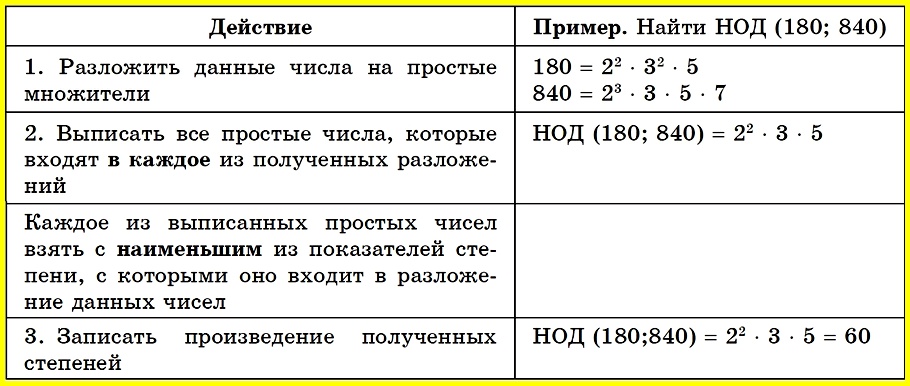
Решение: Нахождение количества учащихся этого класса сводится к нахождению наибольшего общего делителя чисел 155 и 62, поскольку тетради и ручки поделили поровну. 155 = 5 • 31; 62 = 2 • 31. НОД (155; 62) = 31.

Ответ: 31 ученик в классе. [/idea]

Наименьшее общее кратное

Кратным натурального числа а называется натуральное число, которое делится на а без остатка. Например, число 8 имеет кратные: 8, 16, 24, 32, … Любое натуральное число имеет бесконечно много кратных.

Наименьшее общее кратное (НОК) называется наименьшее натуральное число, которое кратно этим числам.

Алгоритм нахождения наименьшего общего кратного (НОК):

[idea]НОК также часто применяется в задачах. Например, два велосипедиста одновременно стартовали по велотреку в одном направлении. Один делает круг за 1 мин, а другой — за 45 с. Через какое наименьшее количество минут после начала движения они встретятся на старте?

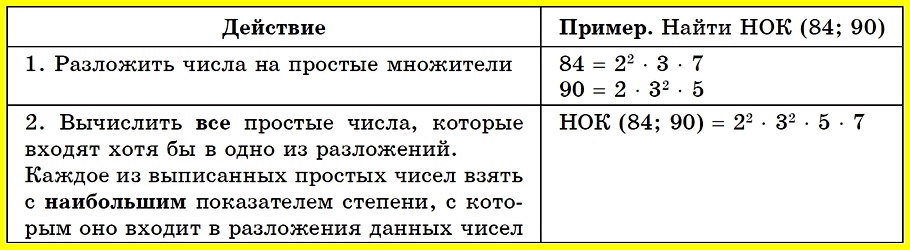
Решение: Количество минут, через которое они снова встретятся на старте, должно делиться на 1 мин,, а также на 45 с. В 1 мин = 60 с. То есть необходимо найти НОК (45; 60).
45 = 3² • 5;
60 = 2² • 3 • 5.
НОК (45; 60) = 2² • 3² • 5 = 4 • 9 • 5 = 180.
В результате получается, что велосипедисты встретятся на старте через 180 с = 3 мин.

Ответ: 3 мин. [/idea]

Деление с остатком

Если натуральное число а не делится нацело на натуральное число b, то можно выполнить деление с остатком. В таком случае полученное частное называется неполным. Справедливо равенство:

а = b • n + r,

где а — делимое, b — делитель, n — неполное частное, r — остаток. Например, пусть делимое равно 243, делитель — 4, тогда 243 : 4 = 60 (остаток 3). То есть а = 243, b = 4, n = 60, r = 3, тогда 243 = 60 • 4 + 3.

Числа, которые делятся на 2 без остатка, называются четными: а = 2n, n ∈ N.

Остальные числа называются нечетными: b = 2n + 1, n ∈ N.

Это конспект по теме «Натуральные числа. Признаки делимости». Чтобы продолжить, выберите дальнейшие действия:

Перейти к следующему конспекту: Обыкновенная дробь
Вернуться к списку конспектов по Математике.
Проверить знания по Математике.

Натуральные числа. Признаки делимости. НОД и НОК