Математика 5 Дорофеев Контрольная № 1

Контрольная работа № 1 по математике в 5 классе «Натуральные числа. Линии» с ответами (4 варианта). Математика 5 Дорофеев Контрольная № 1. Поурочное планирование по математике для 5 класса. Глава 2. НАТУРАЛЬНЫЕ ЧИСЛА. Уроки 19, 20. Контрольная работа по теме «Натуральные числа. Линии». УМК Г.В. Дорофеев и др. (М.: Просвещение).

Смотреть Список всех контрольных по математике в 5 классе (Дорофеев).

Контрольная работа № 1
«Натуральные числа. Линии»

Цель: проверить знания, умения и навыки учащихся по теме.
Тип урока: урок контроля, оценки и коррекции знаний.

ХОД УРОКА

1. Организационный момент

Мотивация к учебной деятельности. Учитель сообщает тему урока, формулирует цели урока.

2. Общая характеристика работы

Контрольная работа составлена в четырех вариантах различной сложности (варианты 1, 2 — самые простые, варианты 3, 4 — несколько сложнее). Каждый вариант содержит 6 задач примерно одинаковой сложности (могут быть немного сложнее две последние задачи).

При проверке вариантов 1, 2 оценка «5» ставится за правильное решение пяти задач, оценка «4» — четырех задач и оценка «3» — трех задач. Одна задача является резервной (или запасной) и дает учащимся некоторую возможность выбора. При таких же критериях оценки в случае решения вариантов 3, 4 дается дополнительно один балл (учитывая более высокую сложность вариантов). Поэтому в случае вариантов 3, 4 оценку «5» можно получить за правильное решение четырех задач.

Выбор вариантов может быть сделан учителем или самим учащимся. Разумеется, учащиеся должны знать о различной сложности вариантов и критериях оценки контрольной работы.

3. Выполнение контрольной работы

K-1. Вариант 1

1. Постройте отрезок АВ длиной 8 см. На этом отрезке выбрана точка С так, что АС = 3ВС. На сколько сантиметров отрезок АС длиннее отрезка ВС?
2. На плоскости построена окружность с центром в точке О и радиусом 5 см. Выбрана точка А так, что ОА = 3 см. Через точку А проведена прямая. В скольких точках эта прямая может пересекать окружность? Сделайте рисунок.
3. Используя по одному разу цифры 0, 3, 8, запишите наименьшее и наибольшее трехзначные числа.
4. Пусть n — любое натуральное число. Каким числом (четным или нечетным) будет число 2n + 5?
5. Для натурального числа n выполнено неравенство 13 < n < 18. Какими могут быть числа n?
6. Сколько трехзначных чисел можно составить, используя только цифры 3 и 8? Выпишите эти числа.

K-1. Вариант 2

1. Постройте отрезок АВ длиной 10 см. На этом отрезке выбрана точка С так, что АС = 4ВС. На сколько сантиметров отрезок АС длиннее отрезка ВС?
2. На плоскости построена окружность с центром в точке О и радиусом 4 см. Выбрана точка А так, что ОА = 4 см. Через точку А проведена прямая. В скольких точках эта прямая может пересекать окружность? Сделайте рисунок.
3. Используя по одному разу цифры 0, 2, 7, запишите наименьшее и наибольшее трехзначные числа.
4. Пусть n — любое натуральное число. Каким числом (четным или нечетным) будет число 2n + 8?
5. Для натурального числа n выполнено неравенство 21 < n <21. Какими могут быть числа n?
6. Сколько трехзначных чисел можно составить, используя только цифры 5 и 7? Выпишите эти числа.

K-1. Вариант 3

1. Постройте отрезок АВ длиной 12 см. Точка С — середина этого отрезка. На отрезке АС выбрана точка D так, что AD = 2DC. На сколько сантиметров отрезок BD длиннее отрезка AD?
2. На плоскости построена окружность с центром в точке А и радиусом 4 см. На этой окружности выбрана точка В. Построена вторая окружность с центром в точке В и радиусом 3 см. Найдите наибольшее возможное расстояние между точками этих окружностей.
3. Используя по одному разу цифры 0, 1, 2, 5 и 8, запишите наименьшее и наибольшее трехзначные числа.
4. Пусть n — любое четное натуральное число. Каким числом (четным или нечетным) будет число 3n + 7?
5. Для натурального числа n выполнены неравенства n > 17 и 12 < n < 21. Какими могут быть числа n?
6. Сколько трехзначных четных чисел можно составить из цифр 0, 1,2, 3, 5, 6, 7 (цифры могут повторяться)?

K-1. Вариант 4

1. Постройте отрезок АВ длиной 12 см. Точка С — середина этого отрезка. На отрезке АС выбрана точка D так, что DC = 2AD. На сколько сантиметров отрезок BD длиннее отрезка AD?
2. На плоскости построена окружность с центром в точке А и радиусом 5 см. На этой окружности выбрана точка В. Построена вторая окружность с центром в точке В и радиусом 2 см. Найдите наибольшее возможное расстояние между точками этих окружностей.
3. Используя по одному разу цифры 0, 3, 4, 6 и 9, запишите наименьшее и наибольшее трехзначные числа.
4. Пусть n — любое нечетное натуральное число. Каким числом (четным или нечетным) будет число 5n + 3?
5. Для натурального числа n выполнены неравенства n <29 и 23 < n < 34. Какими могут быть числа n?
6. Сколько трехзначных нечетных чисел можно составить из цифр 0, 2, 3, 5, 6, 7, 9 (цифры могут повторяться)?

4. Подведение итогов контрольной работы

1. Распределение работ по вариантам и результаты решения. Удобно данные заносить в таблицу (для каждой пары вариантов).

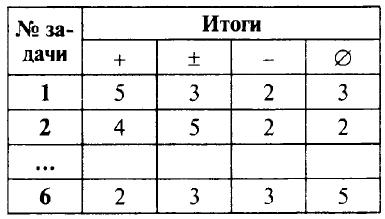
Обозначения:
+ — число решивших задачу правильно или почти правильно;
± — число решивших задачу со значительными погрешностями;
– — число не решивших задачу;
∅ — число не решавших задачу.

2. Типичные ошибки, возникшие при решении задач.
3. Наиболее трудные задачи и их разбор (учителем или школьниками, решившими эту задачу).
4. Ответы ко всем задачам контрольной работы (можно вывесить на стенде).

5. Ответы на задачи контрольной работы

В конце урока учитель раздает на каждую парту краткую запись решения задач контрольной работы.
Домашнее задание: решить задачи, с которыми ученик не справился.

Вариант 1

1. АС – ВС = 4 см.
2. Две точки.
3. 308 и 830.
4. Нечетное число.
5. 14, 15, 16, 17.
6. Числа: 333, 338, 383, 388, 833, 838, 883, 888 (всего 8 чисел).

Вариант 2

1. АС – ВС = 6 см.
2. Одна или две точки.
3. 207 и 720.
4. Четное число.
5. 22, 23, 24, 25, 26.
6. Числа: 555, 557, 575, 577, 755, 757, 775, 777 (всего 8 чисел).

Вариант 3

1. BD – AD = 4 см.
2. 11 см.
3. 102 и 852.
4. Нечетное число.
5. 18, 19, 20.
6. 6 • 7 • 3 = 126 чисел.

Вариант 4

1. BD – AD = 8 см.
2. 12 см.
3. 304 и 964.
4. Четное число.
5. 24, 25, 26, 27, 28.
6. 6 • 7 • 4 = 168 чисел.

Вы смотрели: Контрольная работа № 1 по математике в 5 классе «Натуральные числа. Линии» с ответами (2 уровня сложности по 2 варианта). УМК Г.В. Дорофеев и др. (М.: Просвещение). Поурочное планирование по математике для 5 класса. Глава 2. НАТУРАЛЬНЫЕ ЧИСЛА. Уроки 19, 20. Контрольная работа по теме «Натуральные числа. Линии». Математика 5 Дорофеев Контрольная № 1.

Вернуться к Списку всех контрольных по математике в 5 классе (Дорофеев).