Дискретная форма представления информации
«Дискретная форма представления информации»
Код ОГЭ: 1.1.3 Дискретная форма представления информации. Единицы измерения количества информации
Информация может быть представлена в аналоговой или дискретной форме. Величина в аналоговой форме может принимать бесконечное множество значений. Примерами аналогового представления информации могут служить звук скрипки, картина художника, показатели температуры воздуха, уровня воды в реке.
Величина в дискретной форме может принимать только конечное множество значений. Примеры дискретного представления информации: цифровые показания часов или спидометра, текст в книге, изображение на экране монитора.
Величину в аналоговой форме представления информации можно преобразовать в величину в дискретной форме. Этот процесс называется дискретизацией.
Представление информации в компьютере дискретно. В процессах хранения, обработки и передачи информации в компьютере используется двоичная знаковая система. Ее алфавит состоит всего из двух знаков {0, 1}. Для удобства использования такого алфавита договорились называть любой из его знаков бит (от англ. bit — binary digit — двоичный знак). Поскольку один бит может принимать только одно из двух значений, то им выражают одно из двух взаимоисключающих понятий: да/нет, истина/ложь, включено/выключено.
Способ представления информации с помощью кода из двух знаков оказался наиболее значимым для развития техники. Двоичные числа удобно хранить, обрабатывать и передавать с помощью электронных устройств. Основным носителем информации в них являются элементы, которые могут находиться в одном из двух состояний: включено/выключено, высокий/низкий уровень напряжения или тока, наличие/отсутствие намагниченности материалов. Условно одно состояние обозначают через 1, а другое через 0. Каждый такой элемент способен хранить один двоичный разряд, или бит информации.
Любое информационное сообщение представляется последовательностью нулей и единиц (цифрового кода). Этот метод представления информации называется двоичным кодированием. Таким образом, двоичный код является универсальным средством кодирования информации. Благодаря двоичному кодированию все действия по обработке сообщений компьютером сводятся к совокупности простых действий над 0 и 1.
Единицы измерения количества информации
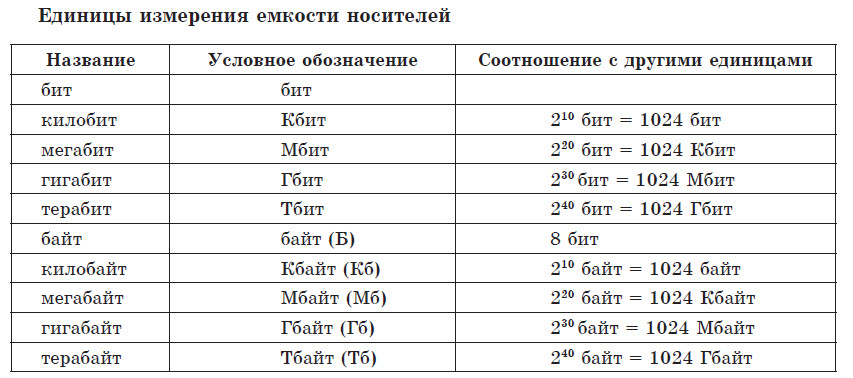
[idea]Бит — единица измерения количества информации, равная одному разряду в двоичной системе счисления. Это наименьшая единица измерения информации.[/idea]Основной единицей хранения и обработки цифровой информации принят байт.
[idea]Байт (англ. byte) — совокупность восьми двоичных разрядов (битов).[/idea]Соответственно, с помощью одного байта можно получить 256 (= 28) двоичных значений (от 00000000 до 11111111). В современных персональных компьютерах байт является наименьшей совокупностью битов, которую компьютер обрабатывает одномоментно.
На практике применяют более емкие, чем байт, единицы измерения объема сообщений и емкости носителей — килобайты, мегабайты, гигабайты, терабайты. Множителем при переходе к более емкой единице измерения выступает число 1024 (= 210).
Системы счисления
Система счисления — совокупность обозначений, приемов и правил для записи чисел цифровыми знаками. В зависимости от способов изображения чисел цифрами системы счисления делятся на непозиционные и позиционные.
Непозиционные системы счисления — такие, в которых количественное значение каждой цифры не зависит от занимаемой ею позиции в изображении числа.
Примером может служить египетская система счисления — в ней иероглифы (цифры), составляющие число, можно записывать сверху вниз, справа налево или вперемежку. Значение числа равно сумме значений цифр в его записи.
Переходной от непозиционных систем к позиционным служит римская система счисления. В ней позиция некоторых цифр уже меняет значение числа: например, в числе IX единицу нужно отнять от десяти, а в числе XI единицу нужно прибавить к десяти. Однако количественное значение самих цифр Х и I от их позиции не зависит.
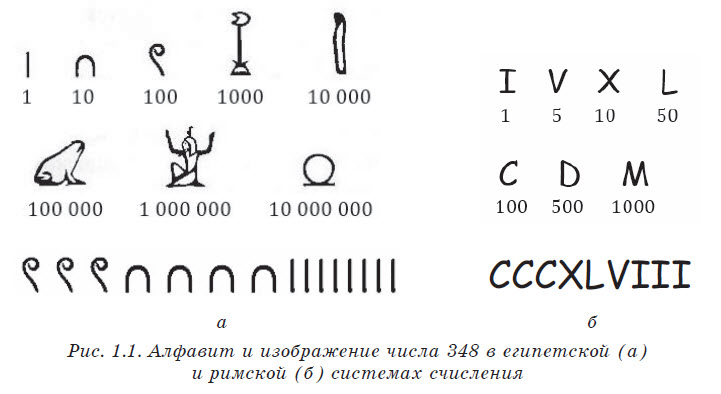
В римской системе цифры записываются слева направо в порядке убывания, и тогда их значения складываются. Если слева записана меньшая цифра, а справа — большая, то их значения вычитаются. Нежелательно записывать более трех одинаковых цифр подряд.
Например, для представления числа 348 в римской системе счисления надо выписать сначала число сотен, затем десятков и единиц: 300 — ССС, 40 — ХL, 8 — VIII. Затем соединить эти записи: CCCXLVIII. Аналогично для числа 1977: 1 тысяча — М, 900 — СМ, 70 — LXХ, 7 — VII. Результат: MCMLXXVII.
В непозиционных системах очень трудно производить многие действия над числами, особенно умножение и деление, слишком громоздка запись для больших чисел. Поэтому широкое распространение получили позиционные системы счисления.
Позиционные системы счисления — такие, в которых количественное значение каждой цифры зависит от ее позиции в числе.
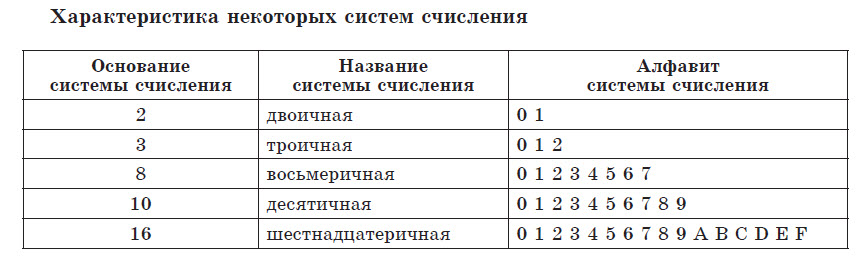
Количество знаков (цифр), используемых для изображения числа, называется основанием системы счисления (или мощностью алфавита). Систему с основанием 10 называют десятичной, с основанием 2 — двоичной, с основанием 16 — шестнадцатеричной, в общем случае: с основанием k — k-ичной.
Место цифры в числе называется разрядом, а количество цифр в числе — его разрядностью. Разряды целого числа нумеруются справа налево начиная с 0. Дробные разряды нумеруют слева направо начиная с -1.
Примером позиционной системы счисления является используемая нами арабская десятичная система счисления. Иногда ее называют индо-арабской, поскольку она была придумана в Индии, а стала известна в Европе из арабских трактатов. Алфавит этой системы составляют 10 цифр — от 0 до 9. Каждая цифра в числе при перемещении справа налево в следующий разряд увеличивает свое значение в 10 раз. Чтобы определить значение числа, надо сложить произведения каждой его цифры на 10 в степени, равной разряду этого числа.
348 = 3 • 102 + 4 • 101 + 8 • 100
–348,17 = –(3 • 102 + 4 • 101 + 8 • 100 + 1 • 10–1 + 7 • 10–2)
Системы счисления могут иметь различные основания. Чтобы различать, в какой системе счисления записано число, принято указывать ее основание в виде нижнего индекса справа от числа. Сам индекс всегда представляется в десятичной системе. Для самой десятичной системы индекс указывают только тогда, когда используется какая–либо другая система:
316 — число в десятичной системе счисления,
3168 — число в восьмеричной системе счисления.
Свойства записи чисел в позиционной системе счисления:
- Для записи чисел в позиционной системе счисления с основанием k требуется k знаков (алфавит системы состоит из k цифр или букв).
- Основание системы счисления, записанное в ней, всегда имеет вид 10 (читается «один ноль»).
- С помощью n разрядов в позиционной системе счисления с основанием k могут быть записаны kn чисел (от 0 до kn–1).
Если основание системы k больше 10, то цифры старше 10 при записи обозначают прописными буквами латинского алфавита: A, B, …, Z. При этом цифре 10 соответствует знак A, цифре 11 — знак B и т. д.

Информация в компьютере представлена в цифровой двоичной форме. В целях экономичного отображения двоичную информацию можно представлять в шестнадцатеричном виде. В программировании часто используется восьмеричная запись чисел.
В общем виде число в позиционной системе счисления может быть представлено как последовательность символов алфавита (цифр), обозначенных через а1, а2, а3 и т. д. Для числа А с количеством целых разрядов n и количеством дробных разрядов m запись имеет вид:
А = an–1 an–2 … а2 а1 а0 а–1 а–2 … a–m
Такая запись называется свернутой записью числа. Эту форму записи мы используем в повседневной жизни, поэтому ее называют также естественной.
Представление числа в виде многочлена называют развернутой записью числа:
А = аn–1 • kn–1 + аn–2 • kn–2 + … + а1 • k1 + а0 • k0 + а1 • k1 + … а–m • k–m.
Развернутая запись числа задает правило для вычисления числа по его цифрам в k–ичной системе счисления. Для уменьшения количества вычислений пользуются схемой Горнера, которая получается путем поочередного выноса основания системы k за скобки:
A = (…((an–1 • k + an–2) • k + an–3) • k + … + а1) • k + а0.
Конспект урока по информатике «Дискретная форма представления информации».
Вернуться к Списку конспектов по информатике.