Алгебра 8 класс: все темы, правила и формулы
Алгебра 8 класс: все темы, правила и формулы.
Краткий курс алгебры за 8 класс.
«Алгебра 8 класс: все темы, правила и формулы» — это краткое повторение алгебры за 8 класс (основные понятия, формулы и определения). Вся информация, самое главное и всё, что нужно знать вкратце. Цитаты взяты из учебника для общеобразовательных учреждений (авт. Ю.Н. Макарычев, Н.Г. Миндюк, К.И. Нешков, С.Б. Суворова под ред. С.А. Теляковского) — М.: Просвещение, 2017.
Выражения и их преобразования
■ 1. Выражения, составленные из чисел и переменных с помощью действий сложения, вычитания и умножения, называют целыми выражениями. При этом произведение одинаковых множителей может быть записано в виде степени. К целым выражениям относят и выражения, в которых, кроме действий сложения, вычитания и умножения, используется деление на число, отличное от нуля. Например, выражения а2 + 3ab – 2b2, (х – у)(2х + у2), m – n/3 целые.
Выражения, составленные из чисел и переменных, в которых, кроме действий сложения, вычитания и умножения, используется деление на выражение с переменными, называют дробными выражениями. Например, выражения х + 1/(x – 1), (a + 2)/b, 5m : n дробные.
Целые и дробные выражения называют рациональными выражениями.
Целое выражение имеет смысл при любых значениях входящих в него переменных. Дробное выражение при некоторых значениях переменных может не иметь смысла. Например, выражение a + 1/(a – 2) не имеет смысла при а = 2, выражение 3/(x – y) не имеет смысла при х = у.
Значения переменных, при которых выражение имеет смысл, называют допустимыми значениями переменных.
■ 2. Тождеством называется равенство, верное при всех допустимых значениях входящих в него переменных.
Два выражения, принимающие равные значения при всех допустимых для них значениях переменных, называют тождественно равными, а замену одного выражения другим, тождественно равным ему, — тождественным преобразованием выражения.
■ 3. Одночленами называют произведения чисел, переменных и их степеней, а также сами числа, переменные и их степени. Например, 8а3b, –1,5xy2z8, 12, с, m10 — одночлены.
Степенью одночлена называется сумма показателей степеней всех входящих в него переменных. Например, степень одночлена 9а7b равна 8.
■ 4. Многочленом называется сумма одночленов. Например, у4 – 8у3 + 2у – 3, 4а4b + 11а2b2 – ab + 3b – 1 — многочлены. Одночлены считают многочленами, состоящими из одного члена.
Степенью многочлена стандартного вида называют наибольшую из степеней входящих в него одночленов. Например, степень многочлена 18а6 – 7а4b3 + 1 равна степени одночлена –7а4b3, т. е. равна 7. Степенью произвольного многочлена называют степень тождественно равного ему многочлена стандартного вида.
■ 5. При сложении многочленов пользуются правилом раскрытия скобок: если перед скобками стоит знак «плюс», то скобки можно опустить, сохранив знак каждого слагаемого, заключённого в скобки. Например, (5х2 – 3ху) + (4ху – 2х2 + 1) = 5х2 – 3ху + 4ху – 2х2 + 1 = = 3x2 + ху + 1.
При вычитании многочленов пользуются правилом раскрытия скобок: если перед скобками стоит знак «минус», то скобки можно опустить, изменив знак каждого слагаемого, заключённого в скобки. Например, (8а2 – 3ab) – (7а2 – 4ab + 5) = 8а2 – 3ab –7а2 + 4аb – 5 = а2 + ab – 5.
Чтобы умножить одночлен на многочлен, нужно умножить этот одночлен на каждый член многочлена и полученные произведения сложить. Например, 2x2(3x3 – ху + 5у2) = 6х5 – 2х3у + 10х2у2.
Чтобы умножить многочлен на многочлен, нужно каждый член одного многочлена умножить на каждый член другого многочлена и полученные произведения сложить. Например, (2а – 3)(3а2 + а – 4) = 6а3 + 2а2 – 8а – 9а2 – За + 12 = 6а3 – 7а2 – 11а + 12.
Любое целое выражение можно представить в виде многочлена.
■ 6. Формулы сокращённого умножения.
а) (а + b)2 = а2 + 2ab + b2.
Квадрат суммы двух выражений равен квадрату первого выражения плюс удвоенное произведение первого и второго выражений плюс квадрат второго выражения.
б) (а – b)2 = а2 – 2ab + b2.
Квадрат разности двух выражений равен квадрату первого выражения минус удвоенное произведение первого и второго выражений плюс квадрат второго выражения.
в) (а + b)3 = а3 + 3а2b + 3ab2 + b3.
Куб суммы двух выражений равен кубу первого выражения плюс утроенное произведение квадрата первого выражения и второго плюс утроенное произведение первого выражения и квадрата второго плюс куб второго выражения.
г) (а – b)3 = а3 – 3а2b + 3ab2 – b3.
Куб разности двух выражений равен кубу первого выражения минус утроенное произведение квадрата первого выражения и второго плюс утроенное произведение первого выражения и квадрата второго минус куб второго выражения.
д) (а – b)(а + b) = а2 – b2.
Произведение разности двух выражений и их суммы равно разности квадратов этих выражений.
е) а3 + b3 = (а + b)(а2 – ab + b2).
Сумма кубов двух выражений равна произведению суммы этих выражений и неполного квадрата их разности.
ж) а3 – b3 = (а – b)(а2 + ab + b2).
Разность кубов двух выражений равна произведению разности этих выражений и неполного квадрата их суммы.
■ 7. Разложением многочлена на множители называют представление многочлена в виде произведения многочленов.
Для разложения многочленов на множители применяют вынесение множителя за скобки, группировку, используют формулы сокращённого умножения. Например, многочлен 8а3 – 6аb можно разложить на множители, вынося 2а за скобки: 8а3 – 6аb = 2а (4а2 – 3b); многочлен 2ab + 10b – За – 15 можно разложить на множители, используя группировку:
2ab + 10b – 3а – 15 = (2аb + 10b) – (За + 15) = 2b(а + 5) – 3(а + 5) = (а + 5)(2b – 3);
многочлен 9а2 – 25b4 можно разложить на множители, используя формулу разности квадратов:
9а2 – 25b4 = (3а)2 – (5b2)2 = (3а – 5b2)(3а + 5b2).
■ 8. Рациональной дробью называется выражение вида a/b, где а и b — многочлены.
При любых значениях а, b и с, где b ≠ 0 и с ≠ 0, верно равенство a/b = ac/bc. Это равенство сохраняет силу и в том случае, когда под буквами а, b и с понимают многочлены, причём b и c — ненулевые многочлены. Свойство дроби, выраженное тождеством a/b = ac/bc называют основным свойством дроби. Основное свойство дроби используется при сокращении дробей. Например: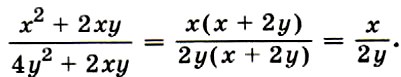
Если изменить знак числителя (или знак знаменателя) дроби и знак перед дробью, то получим выражение, тождественно равное данному:![]()
■ 9. Действия над рациональными дробями выполняются аналогично действиям над обыкновенными дробями.
а) Если с ≠ 0, то![]()
Чтобы сложить дроби с одинаковыми знаменателями, нужно сложить их числители, а знаменатель оставить тем же. Например:![]()
Чтобы выполнить вычитание дробей с одинаковыми знаменателями, нужно из числителя первой дроби вычесть числитель второй дроби, а знаменатель оставить тем же. Например: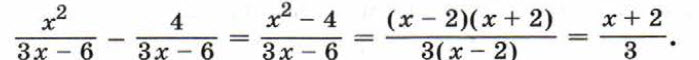
б) Чтобы выполнить сложение или вычитание дробей с разными знаменателями, нужно привести их к общему знаменателю и затем применить правило сложения или вычитания дробей с одинаковыми знаменателями. Например: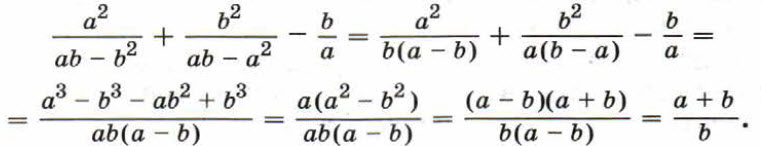
в) Если b ≠ 0 и d ≠ 0, то (a/b)*(c/d) = ac/bd.
Чтобы умножить дробь на дробь, нужно перемножить их числители и перемножить их знаменатели и первое произведение записать числителем, а второе — знаменателем дроби. Например: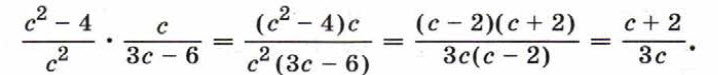
г) Если b ≠ 0, с ≠ 0 и d ≠ 0, то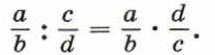
Чтобы разделить одну дробь на другую, нужно первую дробь умножить на дробь, обратную второй. Например:
Любое рациональное выражение можно представить в виде рациональной дроби.
■ 10. Степень с целым показателем.
Если n — натуральное число, большее 1, и а — любое число, то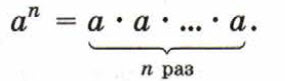
Если n = 1 и а — любое число, то a1 = a.
Если n = 0 и а — число, отличное от нуля, то а0 = 1.
Если n — целое отрицательное число и а — отличное от нуля число, то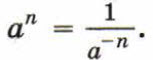
■ 11. Свойства степени с целым показателем.
а) аmаn = аm+n, где а ≠ 0, m и n — целые числа.
При умножении степеней с одинаковыми основаниями основание оставляют прежним, а показатели степеней складывают.
б) аm : аn = аm–n, где а ≠ 0, m и n — целые числа.
При делении степеней с одинаковыми основаниями основание оставляют прежним, а из показателя степени делимого вычитают показатель степени делителя.
в) (аm)n = аmn, где а 0, m и n — целые числа.
При возведении степени в степень основание оставляют прежним, а показатели степеней перемножают.
г) (ab)n = аnbn, где а ≠ 0 и b ≠ 0, n — целое число.
При возведении в степень произведения возводят в эту степень каждый множитель и результаты перемножают.
д) (a/b)n = an/bn, где а ≠ 0 и b ≠ 0, n — целое число.
При возведении в степень дроби возводят в эту степень числитель и знаменатель и первый результат записывают в числителе, а второй — в знаменателе дроби.
■ 12. Квадратным корнем из числа а называется число, квадрат которого равен а.
Арифметическим квадратным корнем из числа а называется неотрицательное число, квадрат которого равен а. Арифметический квадратный корень из а обозначают √a. Выражение, стоящее под знаком корня, называют подкоренным выражением. Выражение √а имеет смысл для всех а ≥ 0 и не имеет смысла при а < 0.
Свойства арифметического квадратного корня.
а) Если а ≥ 0 и b ≥ 0, то![]()
Корень из произведения неотрицательных множителей равен произведению корней из этих множителей.
б) Если а ≥ 0 и b ≥ 0, то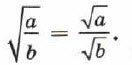
Корень из дроби, числитель которой неотрицателен, а знаменатель положителен, равен корню из числителя, делённому на корень из знаменателя.
в) При любом значении а верно равенство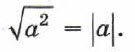
Уравнения
■ 13. Корнем уравнения с одной переменной называется значение переменной, при котором уравнение обращается в верное равенство. Например, число 2 — корень уравнения х3 – х = 4х2 – 10, так как верно равенство 23 – 2 = 4 * 22 – 10.
Решить уравнение с одной переменной — значит найти все его корни или доказать, что корней нет.
■ 14. Уравнения, в которых левая и правая части являются рациональными выражениями, называются рациональными. Если и левая и правая части рационального уравнения являются целыми выражениями, то уравнение называют целым. Рациональное уравнение, в котором левая или правая часть является дробным выражением, называют дробным.
■ 15. Уравнения с одной переменной, имеющие одни и те же корни, называются равносильными. Например, уравнения х2 = 36 и (x – 6)(x + 6) = 0 равносильные. Каждое из них имеет два корня: –6 и 6. Уравнения, не имеющие корней, также считают равносильными.
Уравнения обладают следующими свойствами:
- если в уравнении перенести слагаемое из одной части в другую, изменив его знак, то получится уравнение, равносильное данному;
- если обе части уравнения умножить или разделить на одно и то же отличное от нуля число, то получится уравнение, равносильное данному.
■ 16. Линейным уравнением с одной переменной называется уравнение вида ах = b, где х — переменная, а и b — числа. Число а называется коэффициентом при переменной, число b — свободным членом.
Если а ≠ 0, то уравнение ах = b имеет единственный корень — b/a. Например, уравнение 5х = 3 имеет корень 0,6.
Если а = 0 и b ≠ 0, то уравнение ах = b не имеет корней. Например, уравнение 0 • х = 9 не имеет корней.
Если а = 0 и b = 0, то корнем уравнения ах = b является любое число.
■ 17. Квадратным уравнением называется уравнение вида ах2 + bх + с = 0, где х — переменная, а, b и с — некоторые числа, причём а ≠ 0. Число а называют первым коэффициентом, b — вторым коэффициентом и с — свободным членом.
Квадратное уравнение, в котором первый коэффициент равен 1, называют приведённым квадратным уравнением.
■ 18. Если в квадратном уравнении ах2 + bх + с = 0 хотя бы один из коэффициентов b или с равен нулю, то такое уравнение называют неполным квадратным уравнением.
Неполное квадратное уравнение вида ах2 + bх = 0 имеет два корня: 0 и –b/a. Такие уравнения обычно решают разложением их левой части на множители. Например, 3х2 – 15х = 0, 3х(х – 5) = 0, х1 = 0 и х2 = 5.
Неполное квадратное уравнение вида ах2 + с = 0 имеет два корня: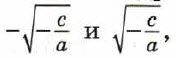
если –c/a > 0, и не имеет корней, если –c/a < 0.
Решают такие уравнения, сводя их к уравнениям вида х2 = m. Например, 0,5х2 – 18 = 0, 0,5x2 = 18, х2 = 36, х1 = –6, х2 = 6.
■ 19. Дискриминантом квадратного уравнения ах2 + bх + с = 0 называют выражение D = b2 – 4ас.
Если D > 0, то квадратное уравнение имеет два корня; если D = 0, то один корень; если D < 0, то квадратное уравнение корней не имеет.
Корни квадратного уравнения ах2 + bх + с = 0 при D ≥ 0 находят по формуле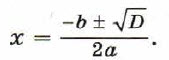
Для квадратного уравнения вида ах2 + kх + с = 0 формулу корней можно записать так: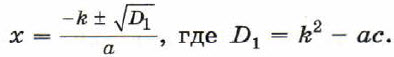
■ 20. Теорема Виета: сумма корней приведённого квадратного уравнения равна второму коэффициенту, взятому с противоположным знаком, а произведение корней равно свободному члену. Иначе говоря, если х1 и х2 — корни уравнения х2 + рх + q = 0, то х1 + х2 = –р и х1х2 = q.
Из теоремы Виета следует, что если х1 и х2 — корни квадратного уравнения ах2 + bх + с = 0, то х1 + х2 = –b/a, х1х2 = c/a.
Теорема, обратная теореме Виета: если числа m и n таковы, что их сумма равна –р, а произведение равно q, то эти числа являются корнями уравнения х2 + рх + q = 0.
■ 21. При решении дробных рациональных уравнений целесообразно поступать следующим образом:
- найти общий знаменатель дробей, входящих в уравнение;
- умножить обе части уравнения на общий знаменатель;
- решить получившееся целое уравнение;
- исключить из его корней те, которые обращают в нуль общий знаменатель.
Решим, например, уравнение![]()
Умножив обе части уравнения на общий знаменатель дробей, т. е. на х(х – 2), получим 2х2 = 2 + х(х + 1). Это уравнение приводится к квадратному уравнению х2 – х – 2 = 0, имеющему корни 2 и –1.
При х = 2 общий знаменатель дробей исходного уравнения обращается в нуль, этот корень нужно исключить. При х = —1 общий знаменатель х(х – 2) в нуль не обращается, следовательно, число –1 является корнем исходного уравнения.
■ 22. Решением уравнения с двумя переменными называется пара значений переменных, обращающая это уравнение в верное равенство. Например, пара чисел х = –5, у = 3 является решением уравнения х2 – 4у = 13. Это решение можно записать так: (–5; 3).
Линейным уравнением с двумя переменными называется уравнение вида ах + by = с, где х и у — переменные, а, b и с — числа.
Уравнения с двумя переменными, имеющие одни и те же решения, называют равносильными. Уравнения, не имеющие решений, также считают равносильными.
■ 23. Каждое решение (х; у) уравнения с двумя переменными можно изобразить в координатной плоскости точкой с координатами х и у. Все такие точки образуют график уравнения.
Графиком линейного уравнения с двумя переменными, в котором хотя бы один из коэффициентов при переменных не равен нулю, является прямая.
■ 24. Решением системы уравнений с двумя переменными называется пара значений переменных, обращающая каждое уравнение системы в верное равенство. Например, пара чисел х = 3, у = 8 — решение системы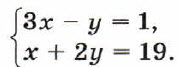
Решить систему уравнений — значит найти все её решения или доказать, что решений нет.
Системы уравнений с двумя переменными, имеющие одни и те же решения, называются равносильными. Системы уравнений, не имеющие решений, также считают равносильными.
Для решения систем уравнений с двумя переменными используются графический способ, способ подстановки, способ сложения.
При графическом способе строят графики линейных уравнений (прямые) и анализируют их расположение:
- если прямые совпадают, то система имеет бесконечно много решений, причём координаты любой точки прямой являются решением системы;
- если прямые параллельны, то система не имеет решений; если прямые пересекаются, то система имеет единственное решение, причём координаты точки пересечения прямых являются решением системы.
При решении системы двух линейных уравнений с двумя переменными способом подстановки поступают следующим образом:
- выражают из какого–либо уравнения системы одну переменную через другую;
- подставляют в другое уравнение системы вместо этой переменной полученное выражение;
- решают получившееся уравнение с одной переменной; подставляют значение найденной переменной в одно из уравнений и находят соответствующее значение другой переменной.
При решении системы двух линейных уравнений с двумя переменными способом сложения поступают следующим образом:
- умножают почленно уравнения системы, подбирая множители так, чтобы коэффициенты при одной из переменных стали в уравнениях противоположными числами;
- складывают почленно левые и правые части уравнений системы;
- решают получившееся уравнение с одной переменной; подставляют значение найденной переменной в одно из уравнений и находят соответствующее значение другой переменной.
Неравенства
■ 25. Число а больше числа b, если разность а – b — положительное число; пишут: а > b. Число а меньше числа b, если разность а – b — отрицательное число; пишут: а < b.
Если а больше b или а равно b, то пишут: а ≥ b. Если а меньше b или а равно b, то пишут: а ≤ b.
Неравенства, составленные с помощью знака > или <, называют строгими. Неравенства, составленные с помощью знака ≥ или ≤, называют нестрогими.
■ 26. Свойства числовых неравенств.
- а) Если а > b, то b < а; если а < b, то b > а.
- б) Если а < b и b < с, то а < с.
- в) Если а < b и с — любое число, то а + с < b + с. Если к обеим частям верного неравенства прибавить одно и то же число, то получится верное неравенство.
- г) Если а < b и с — положительное число, то ас < bс; если а < b и с — отрицательное число, то ас > bс.
Если обе части верного неравенства умножить или разделить на одно и то же положительное число, то получится верное неравенство; если обе части верного неравенства умножить или разделить на одно и то же отрицательное число и изменить знак неравенства на противоположный, то получится верное неравенство.
■ 27. Сложение и умножение числовых неравенств.
а) Если а < b и с < d, то а + с < b + d. Если сложить почленно верные неравенства одного знака, то получится верное неравенство.
б) Если а < b и с < d, где а, b, с и d — положительные числа, то ас < bd. Если перемножить почленно верные неравенства одного знака, левые и правые части которых положительные числа, то получится верное неравенство.
Если а и b — положительные числа, а < b и n — натуральное число, то аn < bn.
■ 28. Решением неравенства с одной переменной называется значение переменной, которое обращает его в верное числовое неравенство. Например, число 1,8 — решение неравенства 5х < 10. Этому неравенству удовлетворяет и любое другое число, меньшее 2.
Решить неравенство с одной переменной — значит найти все его решения или доказать, что решений нет.
■ 29. Неравенства, имеющие одни и те же решения, называются равносильными. Неравенства, не имеющие решений, также считаются равносильными.
Неравенства с одной переменной обладают следующими свойствами:
- если из одной части неравенства перенести в другую слагаемое с противоположным знаком, то получится равносильное ему неравенство;
- если обе части неравенства умножить или разделить на одно и то же положительное число, то получится равносильное ему неравенство;
- если обе части неравенства умножить или разделить на одно и то же отрицательное число, изменив при этом знак неравенства на противоположный, то получится равносильное ему неравенство.
■ 30. Числовой промежуток [а; b], называемый числовым отрезком, — это множество всех чисел х, удовлетворяющих двойному неравенству а ≤ х ≤ b.
Числовой промежуток (а; b), называемым интервалом, — это множество всех чисел, удовлетворяющих двойному неравенству а < х < b.
Числовой промежуток [а; b), называемым полуинтервалом, — это множество всех чисел, удовлетворяющих двойному неравенству а ≤ х < b.
Числовой промежуток (а; b] называемым полуинтервалом, — это множество всех чисел, удовлетворяющих двойному неравенству а < х ≤ b.
Числовые промежутки [а; +оо) и (а; +оо) — это множества всех чисел, удовлетворяющих соответственно неравенствам х ≥ а и х > а.
Числовые промежутки (–oo; b] и (–oo; b) — это множества всех чисел, удовлетворяющих соответственно неравенствам х ≤ b и х < b.
Числовые промежутки [а; +oo) и (–oo; b] называют числовыми лучами, а числовые промежутки (а; +oо) и (–oo; b) — открытыми числовыми лучами.
Числовой промежуток (–oo; +oo) — это множество всех действительных чисел.
■ 31. Неравенства вида ах > b и ах < b, где а и b — некоторые числа, а х — переменная, называются линейными неравенствами с одной переменной.
■ 32. Если ставится задача найти общие решения нескольких неравенств, то говорят, что надо решить систему неравенств.
Решением системы неравенств с одной переменной называется значение переменной, при котором верно каждое из неравенств системы. Решить систему неравенств — значит найти все её решения или доказать, что решений нет.
Функции
■ 33. Зависимость переменной у от переменной х называется функцией, если каждому значению х соответствует единственное значение у. Независимую переменную х иначе называют аргументом, а о зависимой переменной у говорят, что она является функцией этого аргумента. Все значения, которые принимает независимая переменная, образуют область определения функции.
Графиком функции называется множество всех точек координатной плоскости, абсциссы которых равны значениям аргумента, а ординаты — соответствующим значениям функции.
■ 34. Линейной функцией называется функция, которую можно задать формулой вида у = kx + b, где х — независимая переменная, k и b — числа. Её областью определения является множество всех действительных чисел.
Графиком линейной функции является прямая. Число k называют угловым коэффициентом прямой, являющейся графиком функции у = kx + b.
Если k ≠ 0, то график функции у = kx + b пересекает ось х; если k = 0 и b ≠ 0, то прямая у = kx + b параллельна оси х; если k = 0 и b = 0, то график функции совпадает с осью х.
■ 35. Графики двух линейных функций пересекаются, если их угловые коэффициенты различны, и параллельны, если их угловые коэффициенты одинаковы.
■ 36. Линейную функцию, задаваемую формулой у = kx при k ≠ 0, называют прямой пропорциональностью. График прямой пропорциональности есть прямая, проходящая через начало координат. При k > 0 график расположен в первой и третьей координатных четвертях, при k < 0 — во второй и четвёртой координатных четвертях.
■ 37. Обратной пропорциональностью называется функция, которую можно задать формулой вида у = k/x, где х — независимая переменная, k — не равное нулю число. Областью определения функции является множество всех действительных чисел, отличных от нуля.
При k > 0 функция у = k/x принимает отрицательные значения, если х < 0, и положительные значения, если х > 0.
При k < 0 функция у = k/x принимает положительные значения, если х < 0, и отрицательные значения, если х > 0.
График обратной пропорциональности — гипербола. При k > 0 график расположен в первой и третьей координатных четвертях, при k < 0 — во второй и четвёртой координатных четвертях.
■ 38. Областью определения функции у = х2 является множество всех действительных чисел. Функция обращается в нуль при х = 0, а при х ≠ 0 принимает положительные значения. График функции у = х2 — парабола. Этот график проходит через начало координат и расположен в первой и второй координатных четвертях. Он симметричен относительно оси у.
■ 39. Областью определения функции у = х3 является множество всех действительных чисел. Функция обращается в нуль при х = 0, принимает отрицательные значения, если х < 0, и положительные значения, если х > 0. График функции у = x3 проходит через начало координат и расположен в первой и третьей координатных четвертях. Он симметричен относительно начала координат.
■ 40. Область определения функции у = √х — множество всех неотрицательных чисел. Функция обращается в нуль при х = 0, при х > 0 функция принимает положительные значения. График функции у = √х расположен в первой координатной четверти, он представляет собой ветвь параболы.
Действительные числа. Приближённые вычисления
■ 41. Целые и дробные числа составляют множество рациональных чисел. Всякое рациональное число можно представить в виде дроби m/n, где m — целое число, а n — натуральное.
Каждое рациональное число может быть представлено в виде бесконечной десятичной периодической дроби. Каждая бесконечная десятичная периодическая дробь представляет некоторое рациональное число.
Положительные бесконечные десятичные дроби, противоположные им числа и число нуль образуют множество действительных чисел.
Число, которое можно представить в виде бесконечной десятичной непериодической дроби, называют иррациональным числом.
Каждому действительному числу соответствует точка на координатной прямой, и каждой точке координатной прямой соответствует некоторое действительное число.
■ 42. Стандартным видом числа а называют его запись в виде a • 10n, где 1 ≤ а < 10 и n — целое число, число n называют порядком числа. Например, 73 000 = 7,3 • 104; 0,0026 = 2,6 • 10–3.
■ 43. Абсолютной погрешностью приближённого значения числа называется модуль разности точного и приближённого значений. Например, абсолютная погрешность приближённого значения 0,3 числа 1/3 равна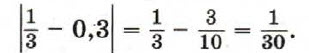
Если абсолютная погрешность приближённого значения не превосходит некоторого числа h, то это значение называют приближённым значением с точностью до h. Например, 1,41 является приближённым значением √2 с точностью до 0,01.
Если число х равно а с точностью до h, то пишут: х = a ± h. При этом число h обычно берут с одной или двумя значащими цифрами. Например, √3 = 1,73 ± 0,01.
■ 44. Относительной погрешностью приближённого значения называется отношение абсолютной погрешности к модулю приближённого значения.
Относительную погрешность обычно выражают в процентах. Например, при округлении дроби 25,4 до единиц получается приближённое значение 25. Его относительная погрешность равна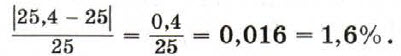
Элементы статистики
■ 45. При анализе данных используются различные статистические характеристики: среднее арифметическое, мода, медиана, среднее гармоническое.
Средним арифметическим ряда чисел называется частное от деления суммы этих чисел на число слагаемых. Например, среднее арифметическое ряда чисел 26, 29, 31, 43, 57, 63 равно![]()
Модой ряда называется число, которое встречается в ряду чаще других. Например, модой ряда чисел 26, 18, 43, 16, 18, 21, 18, 17 является число 18.
Ряд может иметь более одной моды, а может не иметь моды совсем. Например, ряд чисел 34, 38, 41, 19, 41, 38, 35, 21 имеет две моды: 38 и 41, а ряд чисел 19, 27, 29, 35, 37, 41, 43, 49 не имеет моды.
Медианой упорядоченного ряда чисел с нечётным числом членов называется число, записанное посередине этого ряда, а медианой упорядоченного ряда чисел с чётным числом членов называется среднее арифметическое двух чисел, записанных посередине этого ряда.
Например, медиана ряда чисел 17, 21, 27, 29, 32, 37, 41 равна 29, а медиана ряда чисел 28, 43, 54, 56, 58, 62 равна 55.
Медианой произвольного ряда чисел называется медиана соответствующего упорядоченного ряда.
Размахом ряда чисел называется разность между наибольшим и наименьшим из этих чисел. Например, размах ряда чисел 173, 117, 286, 299, 105, 304, 318 равен разности 318 – 105, т. е. равен 213.
Средним гармоническим ряда положительных чисел а1, a2, …, аn называется число аср, которое вычисляется по формуле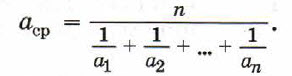
■ 46. Вся изучаемая совокупность данных называется генеральной совокупностью. В случаях, когда сложно или даже невозможно провести сплошное исследование генеральной совокупности, составляется выборочная совокупность (выборка), которая подвергается исследованию. При этом выборка должна быть репрезентативной (представительной), т. е. достаточной по объёму и отражающей характерные особенности исследуемой генеральной совокупности.
■ 47. Для обобщения и систематизации данных, полученных в результате исследования, иногда их по какому–либо признаку разбивают на группы и результаты группировки представляют в виде таблицы частот или относительных частот.
Если в ряду чисел имеется большое число данных и одинаковые данные встречаются редко, то для анализа данных образуют интервальный ряд, указывая для каждого интервала соответствующую частоту или относительную частоту.
■ 48. Для наглядного представления данных, полученных в результате статистического исследования, используют столбчатые и круговые диаграммы, полигоны и гистограммы.
Вы смотрели «Алгебра 8 класс: все темы, правила и формулы» — это краткое повторение алгебры за 8 класс (основные понятия, формулы и определения). Краткий курс алгебры в 8 классе: вся информация, самое главное и всё, что нужно знать вкратце.