Опорные задачи по теме УГЛЫ
Опорные ЗАДАЧИ по теме УГЛЫ
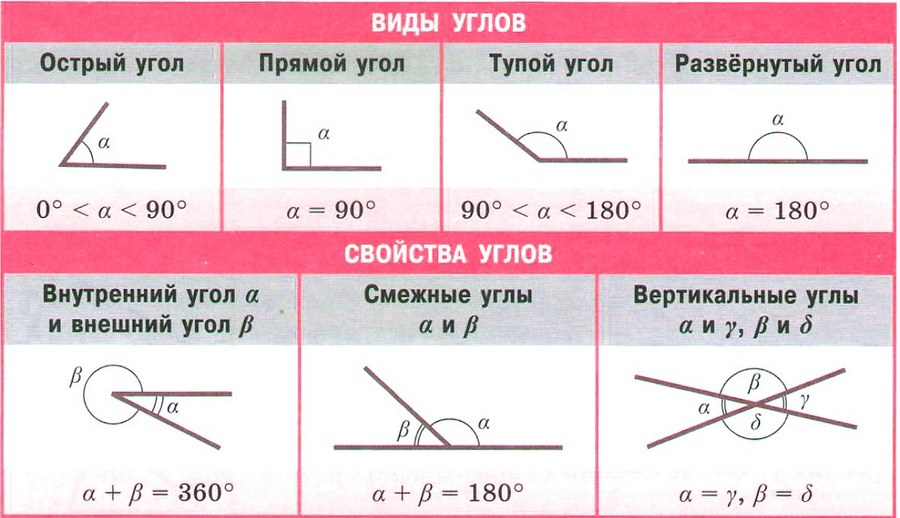
Угол — фигура, образованная двумя лучами, которые выходят из одной точки (вершины). Биссектриса — луч, который выходит из вершины угла и делит его пополам.
Смежные углы — два угла, у которых одна сторона общая,а две другие стороны являются дополняющими лучами. СВОЙСТВА: Сумма смежных углов равна 180°. Два смежных углы образуют развернутый угол. Если два угла равны, то смежные с ними углы тоже равны. Угол, смежный с прямым углом, является прямым. Угол, смежный с острым углом, тупой. Угол, смежный с тупым углом, является острым. Любой луч, исходящий из вершины развернутого угла и проходит между сторонами разделяет его на два смежные углы. Если два угла равны, то смежные с ними углы также равны. Два угла, смежные с одним и тем же углом, уровне. Если два смежных углы равны, то они прямые.
Вертикальные углы — два угла, стороны одного из которых являются дополняющими лучами сторон другого. СВОЙСТВА: Вертикальные углы равны. При пересечении двух прямых образуются две пары вертикальных углов и четыре пары смежных углов.
ПРИМЕРЫ РЕШЕНИЯ ОПОРНЫХ ЗАДАЧ:
Задача № 1. Дано: ∠ABO и ∠OBC – смежные углы, OB – луч, ∠OBC больше ∠ABO в 4 раза. Найти: ∠ABO, ∠OBC.
Задача № 2. Дано: ∠1 и ∠2 – смежные, ∠2 равен 25 % от ∠1. Найти: ∠2, ∠1.

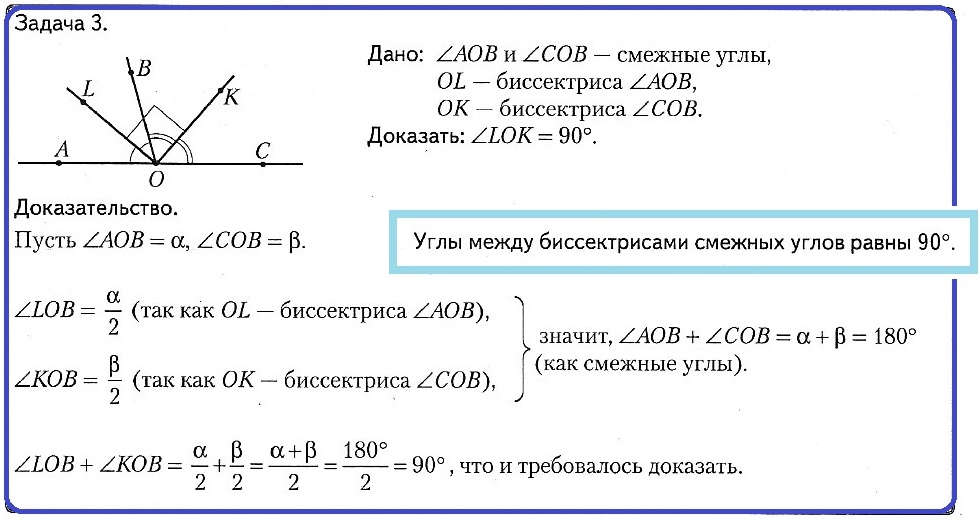
Задача № 3. Дано: ∠AOB и ∠COB – смежные углы, OL – биссектриса ∠AOB, OK – биссектриса ∠COB. Доказать: ∠LOK = 90°.
Задача № 4. Дано: a ∩ b = 0, ∠1 + ∠2 + ∠3 = 210°. Найти: ∠1, ∠2, ∠3, ∠4.

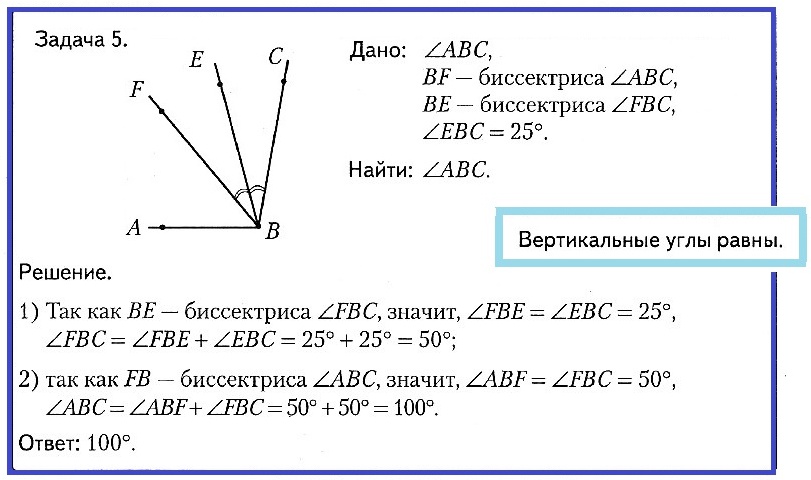
Задача № 5. Дано: ∠ABC, BF – биссектриса ∠ABC, BE – биссектриса ∠FBC, ∠EBC = 25°. Найти: ∠ABC.
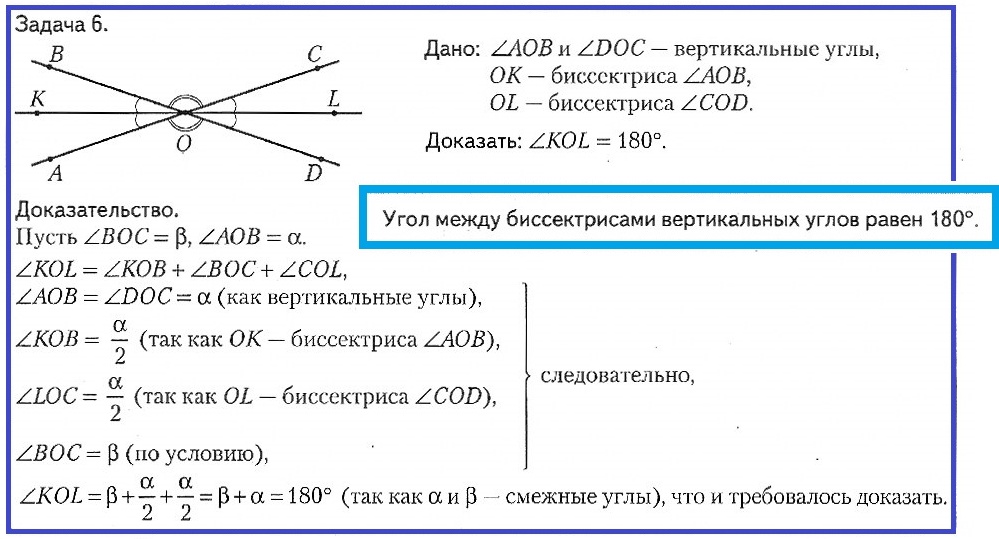
Задача № 6. Дано: ∠AOB и ∠DOC – вертикальные углы, ОК – биссектриса ∠AOB, 0L – биссектриса ∠COD. Доказать: ∠KOL = 180°.
Вы смотрели «Опорные задачи по теме УГЛЫ». Выберите дальнейшие действия:
- Перейти к следующему конспекту: Параллельные прямые
- Проверить знания по Математике.